Considere a função dada por
![]()
- Construa o gráfico de ;
Passo 1
Adorooo ver vocês aqui! Como vocês estão?
Bora gabaritar mais essa questão? Vamos lá!
O enunciado nos diz que é uma função com o domínio e o contradomínio estão contidos no conjunto dos números reais. E depois o enunciado fala que função é uma função definida por partes. Isso quer dizer que de acordo com o que eu escolho, existe uma equação diferente para representar a função , então basicamente indica que a função muda de “identidade” Desse modo, é necessário ter atenção nesse fato quando esboçarmos cada trecho do nosso gráfico.
Passo 2
Galera, como já foi mencionado, a função é definida por partes. Então, isso significa que o nosso gráfico também será esboçado por partes.

Calma!!! Basicamente significa que vamos separar o gráfico final em esboços menores para depois juntarmos. CONFIA rs!
De início vamos pegar o intervalo onde . Se , então será :.
Hummm, temos aqui uma função modular, e isso foi perceptível pela presença do módulo na função. Blz?
Bom dentro do módulo, temos uma função quadrática, certo? e no que isso vai me ajudar? Basicamente o meu gráfico será uma função quadrática porém sem partes negativas.
E aí, complicou? vamos sem desespero fazer o esboço da função quadrática:
Utilizando a fórmula de bhaskara, temos que as raízes dessa função são .
E o gráfico cortará o eixo y quando , ou seja,
Agora temos tudo para fazer o nosso esboço da função quadrática!
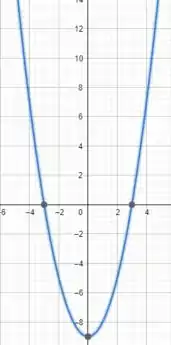
Passo 3
Mas sabemos que quando qualquer número está dentro de um módulo, o resultado sempre será positivo né? Logo, significa que no gráfico de uma função modular não se pode ter partes negativas.
Ora ora, e agora?

A solução é simples!!!
Basta refletirmos essa parte do gráfico situado no 3° e 4° quadrante para cima, exatamente como se fosse colocado um espelho naquela região ali. Assim, o nosso esboço para o intervalo onde será:
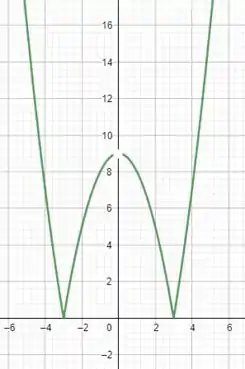
Passo 4
E por fim, para , a nossa função será 9, e pode isso?

Pode simmm! Isso significa apenas que quando o , a nossa função será constante e igual a 9. Desse modo, o esboço dessa parte é apenas um ponto de coordenadas .
Passo 5
Vamos para o fim da nossa questão?

Agora basta que juntemos os esboços dos passos anteriores em um único plano cartesiano. Assim, o gráfico da função será:
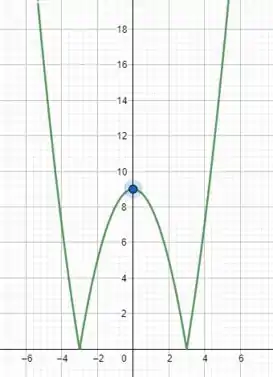
E aí, xuxus? Tudo belezinha?
Bons Estudos!
E bebam água!
Resposta
Resolução nos passos acima