Considere a função dada por
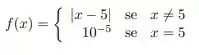
b) Calcule os seguintes limites, justificando suas respostas:
Passo 1
Fala aí galera, beleza? Show!
Amores, a questão nos dá uma função que possui o domínio e imagem no conjunto dos números reais. E a função em questão é uma função definida por partes, ou seja, dependendo do intervalo a equação da nossa função pode mudar. Ok?

Calma e paciência!
Desse modo, vemos que quando o a função será definida como .
Já quando o a função será constante e igual a .
Passo 2
Todavia, o que a questão quer é o limite de quando . Logo, devemos descobrir para onde essa função tende quando nos aproximamos do de ambos os lados, ou seja, devemos descobrir se os limites laterais coincidem e se a função em questão é contínua. Caso um desses dois critérios não seja atendido declaramos que o limite da função não existe. Bora lá!

Passo 3
Primeiramente, verificaremos se a função é contínua. Pela definição matemática, uma função é contínua num ponto se:
Tranquilo, essa relação é pra quando a função for contínua em um ponto certo? Aí você deve tá se perguntando então quando é que a função é completamente contínua? É quando essa regrinha é válida em todo o seu domínio, certo?
Observa-se que quando os limites laterais se aproximam do , a função tende ao valor :
Beleza! Isso significa que os limites laterais são iguais!
Contudo,
Já que
Passo 4
Portanto, o Não Existe!
E aí? Deu pra te ajudar? Responde aí!
Se hidratem!
E bons estudos!
Resposta
Não Existe!
Resposta
Ei, a resposta está no passo a passo :)