UFU, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profª Sonia Berrios - Lista 2 - Limites, Continuidade e Derivadas, Questão 6ii
Defina se é contínua em
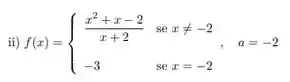
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Calc 1!!! Queremos verificar se a função
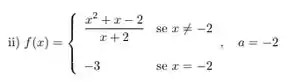
é contínua em . Show?
Bem, vamos lembrar que para uma função ser contínua em um ponto precisamos que
Então vamos calcular esse limite e ver se ele é igual a -3
Passo 2
Vamos verificar os valores de para
Ou seja, para os pontos onde , a nossa função se comporta como a reta .
Logo, ao analisarmos o limite da função quando temos:
Logo, como o valor da função em é o mesmo que o valor do limite nesse ponto. A função é contínua
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento Acima
Exercícios de Livros Relacionados
Explique por que a função é descontínua no dado número a . Esboce o gráfico da função. f x = x 2 - x x 2 - 1 , x ≠ 1 1 , x = 1 ,a = 1
Localize as descontinuidades da função e ilustre com um gráfico. y = ln t g 2 x
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. R x = x 2 + 2 x - 1
Use a definição de continuidade e propriedades dos limites para demonstrar que a função é contínua em um dado número a . f x = x 2 + 7 - x , em a = 4 .
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. F x = s e n - 1 ( x 2 - 1 )