Determine, se existirem, valores de para os quais a função abaixo seja contínua:
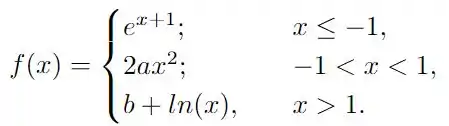
Passo 1
Eaew, beleza?
O enunciado nos dá a seguinte função
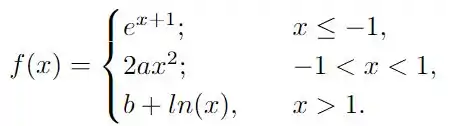
e quer que verifiquemos se existem que garantam a continuidade desta função! Note que os possíveis locais de descontinuidade são e , portanto, vamos tentar verificar se existem tais que
e
assim como
e
Bora lá!
Passo 2
Vamos começar com a possível descontinuidade em , se fizermos o limite pela esquerda, temos que os valores de são menores que , portanto, o limite é da forma
e, portanto, temos que
Agora, se analisarmos o limite pela direita, estamos considerando valores levemente maiores que , portanto, temos que
ou seja, o limite resulta em
Portanto, temos que para que tenhamos a continuidade em , precisamos que , pois então teríamos que
e como, temos que
a função é contínua neste ponto! Vamos analisar agora o outro ponto!
Passo 3
Agora, calculando o limite em , estaremos considerando valores levemente menores que , portanto, o limite se torna
em que usei . Agora, pela direita, temos valores levemente maiores que , portanto, o limite se torna
como temos que . Portanto, para termos que para manter a continuidade precisamos que . De forma, que
O enunciado não deixa claro se pertence ao limite superior ou intermediário, mas isso é indiferente, para ambos, se e , temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e