UNICAMP, Sem Campus, Listas de Cálculo 1 -Lista 3 - Limite e Continuidade, Questão 33
Determine L para que a função seja contínua no ponto dado. Justifique.
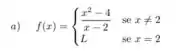
em p = 2
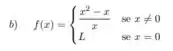
em p = 0
Passo 1
Eaew, belezinha?
Temos que determinar . Para que a função seja contínua temos que deve atender a seguinte condição:
.
Isso garante que a função não seja descontinua.Então, vamos calcular esse limite para as duas situações:
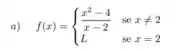
em p = 2
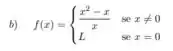
em p = 0.
Vamos lá!
Passo 2
Vamos começar calculando o limite para o item a, para isso vamos fatorar o numerador da função:
.
Então no item a, para que a função seja contínua .
Passo 3
Calculando o limite para o item b:
.
Então no item a, para que a função seja contínua .
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
; .