USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 2.2d
Determine os pontos de continuidade da função
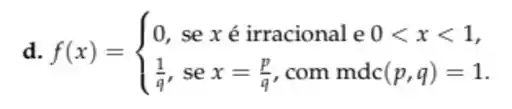
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 1.
Queremos encontrar os pontos de de continuidade da função
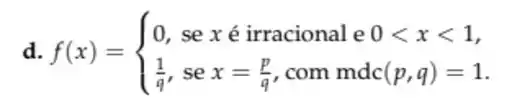
Bem, essa função é meio estranha. Ela vale para os irracionais entre zero e 1, e vale se for racional escrito na forma irredutível
Como podemos verificar seus pontos de continuidade?
Passo 2
Bem, f é descontínua em todos os números racionais: como os irracionais são densos nos reais, para qualquer racional x, não importa que escolha de ε nós façamos, há um irracional a ainda mais próximo deste x, onde (enquanto que é positiva).
Para demonstrar a continuidade nos irracionais, suponha sem perda de generalidade que ε é racional (para qualquer irracional ε', podemos escolher um racional ε" menor ainda). Como ε é racional, ele pode ser expresso como uma fração irredutível . O objetivo é mostrar que é contínua quando é irracional.
Observe que f assume o valor máximo 1 em cada inteiro, pois um número inteiro é escrito como
então podemos limitar nosso exame do intervalo entre.
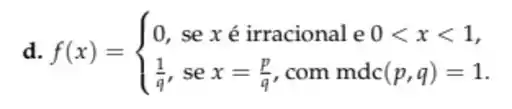
Como ε tem um denominador finito , os únicos valores para os quais f pode retornar um valor maior do que ε são aqueles com um denominador que não é maior do que b. Existe apenas um número finito de valores entre dois números inteiros, com um denominador que não é maior do que b, então estes podem ser listados exaustivamente. Definindo δ como sendo menor do que a menor distância de x a um desses valores, fica garantido que a todo valor a uma distância de no máximo δ de x satisfaz .
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊