UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cáclulo 2 - Profº Félix Gómez - Primeira Lista, Questão 4.2d
Determine a região de continuidade de e trace o esboço, mostrando com uma região sombreada em a região de continuidade de :
d)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a região de continuidade da função e mostrar o gráfico dela. Pra isso, vamos avaliar o domínio da nossa função e descobrir as possíveis restrições desse domínio, que são os valores que e não podem assumir.
A primeira vista, nós temos uma função racional, que em geral é contínua para todo o domínio em . Mas a gente sabe que não pode ter divisão por zero e que não existe raiz quadrada de número negativo dentro dos números reais. Então, a nossa restrição será:
Vamos lá!
Passo 2
Como , temos:
Dividindo todo mundo por :
Então, o domínio da função tá dentro da hipérbole definida por . Portanto, nossa região de continuidade, será dado pelo domínio:
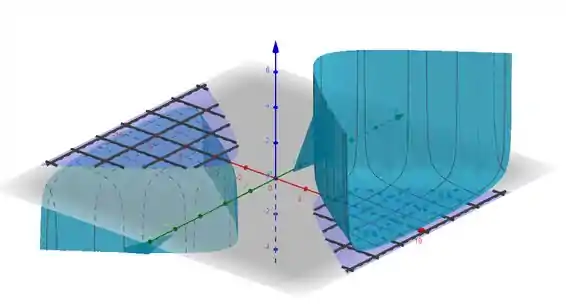
Observando o gráfico de , a gente consegue ver que a região realmente é contínua dentro da hipérbole hachurada em lilás:
Valeu, galera! Até a próxima! 😉