UFU, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profª Sonia Berrios - Lista 2 - Limites, Continuidade e Derivadas, Questão 8
Determine os valores de que tornam a função abaixo contínua em toda parte
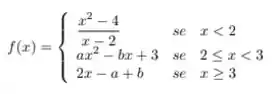
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Calc 1!!! Queremos osvalores de que tornam a função abaixo contínua em toda parte.
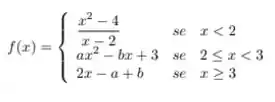
Para a função ser contínua precisamos que os pontos de função satisfaçam
para todo no domínio de
Passo 2
Para encontrarmos os pontos de descontinuidade da função
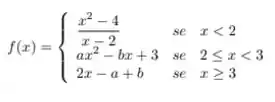
Nossa função é composta de funções contínuas, logo, só precisamos nos preocupar com os pontos onde a troca sua lei de formação para verificarmos a continuidade.
Começando com o ponto . Para a função ser contínua nesse ponto precisamos que
Ou seja, precisamos que
fazendo o limite, temos:
logo temos que ter
Passo 3
Agora, vamos analisar a continuidade no ponto . Para a função ser contínua nesse ponto precisamos que
Ou seja, precisamos que
fazendo o limite, temos:
Ou seja, temos as seguintes condições
Resolvendo esse sistema, obtemos que
Com esses valores de nossa função é contínua
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊