Diga em qual região as funções abaixo são contínuas. Se ela for descontínua em um ponto ou região, diga o motivo da descontinuidade.
c)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar onde a função é contínua e se ela tem alguma descontinuidade.
Bom, pra que uma função seja contínua em um ponto , seu limite precisa existir e ser igual ao valor da função no ponto:
Mas a gente quer saber se existem descontinuidades em todo domínio. Então, primeiro temos que verificar o domínio da função. E pra verificar o domínio, temos que verificar se existem restrições para . Assim, temos que garantir que:
- nas frações o denominador não pode valer zero;
- dentro das raízes quadradas não pode ter n��mero negativo;
- o valor dentro de um logaritmo tem que ser estritamente positivo.
Se houverem restrições, vamos verificar as condições de continuidade nesses pontos do domínio.
Vamos lá!
Passo 2
Vamos começar verificando o domínio da nossa função . Nós temos uma fração e nós sabemos que o denominador dela não pode ser zero. Dessa forma, nossa única condição seria:
Só que a função exponencial já é sempre diferente de zero, por definição. Observe o gráfico abaixo e repare que ela nunca toca o plano :
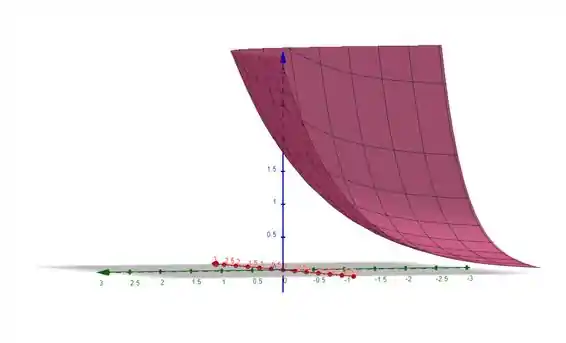
Nosso domínio será:
Sendo assim, nossa função não apresenta descontinuidades e está definida para todo .
Valeu, galera! Até a próxima! 😉