UFCG – Cálculo Diferencial e Integral I – AV1, 2021.2 – 1c
Encontre o domínio das seguintes funções:
c)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função e pediu pra gente encontrar o domínio dela. Mas o que é o domínio de uma função?
O domínio de uma função é o conjunto de todos os valores possíveis que a variável independente da função pode assumir. E quem é a variável independente?
Bom, no nosso caso, como temos uma – uma função que depende de – logo, nossa variável independente é o . Então, quais são os valores que pode assumir na função? Ou melhor, quais são os valores que não pode assumir na função para garantir sua existência?
Passo 2
Os valores que não pode assumir na função são as chamadas restrições. O domínio nem sempre vai ser um conjunto completo, muitas vezes, a variável independente não poderá assumir alguns valores específicos. Mas quais seriam esses valores?
No nosso caso, temos a função:
Para pensar em quais valores pode ou não assumir, vamos pensar nas restrições da função.
Nós temos uma raiz quadrada, lembra que não existe raiz quadrada de número negativo? Então, para garantir a existência da função, tudo que tá dentro da raiz tem que ser maior ou igual a zero (ou seja, positivo). E daí temos nossa restrição:
Para encontrar os valores de vamos resolver essa equação do segundo grau.
Passo 3
Na equação , temos , e . Usando a equação de Bhaskara:
Substituindo os valores:
Assim, vamos ter:
Repara que temos , então . Isso, na equação do segundo grau, significa que ela tem concavidade para cima. Com essas informações a gente consegue fazer um esboço do gráfico, só pra visualizar onde a função é positiva e negativa. Temos:
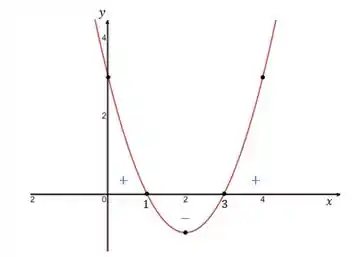
Pra gente agora só importa os dois pontos e . Repara no gráfico que antes de , a função é positiva, depois, até , ela passa a ser negativa. E depois de , a função é positiva de novo.
Lembra que nós falamos no passo , que a função precisa ser positiva? Mas dentro da nossa restrição, nós encontramos e . Então, isso significa que para a função ser positiva:
ou
Juntando tudo, nós temos o domínio da função:
É isso, galera. Valeu! 😉