Encontre valores apropriados para e de modo que a função
seja derivável em e faça um esboço do gráfico de .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para encontrarmos os valores de e da seguinte função:
Para que ela seja derivável em .
Para que isso ocorra, a derivada da função para deve ser igual a derivada da função para .
Em outras palavras, devemos igualar as derivadas no ponto .
E aí? Bora lá??!!
😉
Passo 2
Assim, pela regra da potência, temos:
Assim, no ponto , temos que
E
Logo, no ponto , vemos que .
Passo 3
Assim, igualando as derivadas no ponto , temos:
Descobrindo o valor de :
Assim, temos que
Esboçando o gráfico, temos:
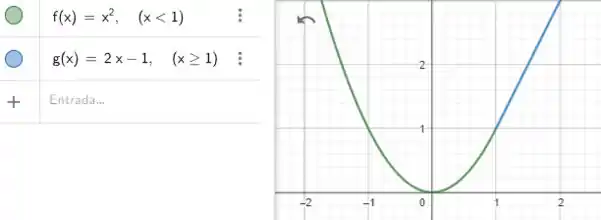
Entendeu direitinho? Responde aee ;)
