UFMG, Sem Campus, Cálculo 1, P1 - 2023.1, Questão 2b
Existe um valor tal que a função
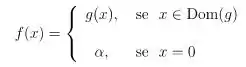
seja contínua em ?
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Calc 1!!! Queremos
verificar a condição para a função
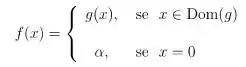
ser contínua em
Vamos nessa!
Passo 2
Para a função ser contínua em precisamos que
Vamos calcular
Multiplicando e dividindo por
Calculando o limite,
Logo, se fizermos
nossa função será contínua em
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento Acima
Exercícios de Livros Relacionados
Explique por que a função é descontínua no dado número a . Esboce o gráfico da função. f x = x 2 - x x 2 - 1 , x ≠ 1 1 , x = 1 ,a = 1
Localize as descontinuidades da função e ilustre com um gráfico. y = ln t g 2 x
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. R x = x 2 + 2 x - 1
Use a definição de continuidade e propriedades dos limites para demonstrar que a função é contínua em um dado número a . f x = x 2 + 7 - x , em a = 4 .
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. F x = s e n - 1 ( x 2 - 1 )