UFF, Cálculo IA-Lista 3, GMA, 2008-1, Questão 15
Para a função definida por
a) Determine os valores de e para que seja contínua em .
b) Esboce o gráfico de .
Passo 1
Vamos começar com a letra (a). Para que a função seja contínua no ponto, precisamos que os limites laterais sejam iguais e iguais ao valor da função, no ponto, ou seja:
Vamos calcular cada um, em cada ponto. Para que a função seja contínua em , precisamos que:
Temos que, como a expressão da função é à esquerda de :
Como não há indeterminação:
Seguindo a mesma ideia, temos que:
E:
Precisamos então que:
Para que a função seja contínua nesse ponto. Temos duas incógnitas e uma equação, precisamos de mais uma para resolver. Vamos analisar o ponto para obter outra equação e matar a questão.
Passo 2
Para esse ponto, precisamos que:
Onde:
Portanto, precisamos que:
Passo 3
Legal, agora temos duas equações e duas incógnitas, já dá para resolver.
Substituindo :
Voltando a primeira equação:
Esses são os valores de e para que a função seja contínua nos pontos e . Garantimos que ela é contínua nos demais pontos do domínio, pois as expressões são sempre contínuas para todos seus domínios.
Passo 4
Vamos agora para a letra , que não tem muito mistério. Para a primeira expressão, temos uma raiz negativa que que vale quando corta o eixo .
A reta será que corta o eixo em:
E o eixo em:
A expressão do módulo será uma parábola com a parte negativa espelhada, uma vez que está dentro de um módulo e o módulo é sempre positivo. Esboçando cada uma expressões e limitando os intervalos, chegamos a:
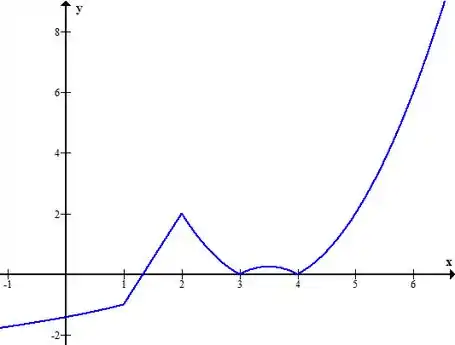
Repare que a função é de fato contínua em todo seu domínio.
Resposta
