A função maior inteiro é a função que associa, a cada elemento , o valor que é o maior número inteiro que é menor ou igual a . Por exemplo,
a) Calcule com
(b) Estude os limites laterais da função maior inteiro no ponto . Em seguida, decida se ela é contínua neste ponto
(c) Determine todos os pontos onde a função não é contínua
(d) Faça um esboço do gráfico da função
Passo 1
Faaala galerinha, vamos pra cima!! Trabalhando agora com a função maior inteiro e seus limites.
- Ora, pela definição de função maior inteiro, podemos afirmar que:
- Se o número tiver parcela decimal, o valor é o maior número inteiro que é menor a .
- Se o número for inteiro, então
- Observemos:
- Pensemos um pouco pra essa parte:
Portanto:
Ao nos aproximarmos de 2 pela esquerda temos valores como [[1.5]], [[1.75]], [[1.99]] e sabemos que esses valores correspondem a 1. Então:
Ao nos aproximarmos de 2 pela direita temos valores como [[2.5]], [[2.25]], [[2.01]] e sabemos que esses valores correspondem a 1. Então:
Concluímos então que o limite não existe e, portanto, a função não é contínua no ponto.
Passo 2

Na linha de raciocínio que estabelecemos na letra b, nenhum ponto pertencente aos inteiros caracterizaria limite existente, muito menos continuidade. No entanto, se analisarmos um valor pra x que difere desse conjunto, como por exemplo:
Temos que se nos aproximamos de 1.5 pela esquerda ou direita teremos valores como [[1.4]] = [[1.49]] = [[1.51]] = [[1.6]] = 1. Logo:
E isso se estende para qualquer número real que foge da intercessão entre o conjunto dos inteiros e racionais.
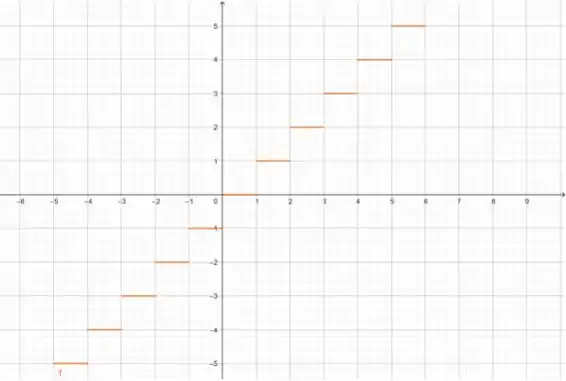
Finalizado, meu povo:

Resposta
- para todo
- .
- A função é descontínua em todos os pontos .
Logo, a função não possui limite definido nem é contínua.