UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Prof° Ricardo Martins - Listas sobre Limites e Continuidade, Questão 2.1
Mostre que a função abaixo não é contínua na origem (tente procurar um e veja o que acontece)
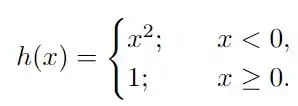
Passo 1
Eaew, tudo certinho contigo?
Aqui o enunciado nos pede para analisar a continuidade da função
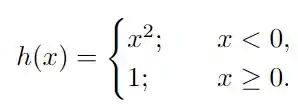
em . Normalmente, eu seguiria pelo caminho de analisar a definição de continuidade em termos de limites! Mas, como a questão pede para tentarmos procurar um , vamos usar a seguinte definição de continuidade
em que e . Ou seja, vamos procurar valores de e arbitrariamente pequenos que garantam a continuidade da função em . Será que isso é possível? Saca só!
Passo 2
Usando então que , temos que
como para , temos que , podemos escrever
ou seja, como temos funções modulares, e devem obedecer os seguintes intervalos
e, também
Vamos tentar escolher um valor de agora!
Passo 3
Se eu escolher um valor de , temos que está no intervalo
Se escolhermos no intervalo
temos que , por exemplo, , obtemos que
nos leva ao intervalo
mas se escolhermos , temos que , e portanto, o intervalo se torna
Note que para valores de dentro do mesmo intervalo, uma mesma escolha de não é suficiente. Se eu escolho , temos que apenas o segundo intervalo é obedecido, note que
e
Sendo assim, não importa o quão pequeno seja o valor de , nunca conseguiremos encontrar um valor de que garanta a definição formal de continuidade. Ou seja, a função é descontínua! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!