UNICAMP – Cálculo 1 – Provas Antigas – P1 – 2022.1 - 6ª Noturno – Questão 5
Mostre que o polinômio possui pelo menos uma raíz real.
Passo 1
Eaeeee, belezinha??? Vamos primeiro atribuir dois valores de para esse polinômio:
Para :
Para
Ooopaa!! Perceba que no intervalo a função passa por um zero (ou uma raiz), né?
Passo 2
Para enxergar melhor, vamos plotar o gráfico:
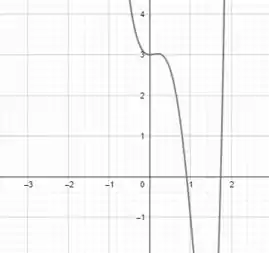
Olha aí!!! Podemos então concluir que há um número real entre e que faz com que o polinômio tenha pelo menos uma raiz real!!!
Entendeu direitinho? Responde aee ;)
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Explique por que a função é descontínua no dado número a . Esboce o gráfico da função. f x = x 2 - x x 2 - 1 , x ≠ 1 1 , x = 1 ,a = 1
Localize as descontinuidades da função e ilustre com um gráfico. y = ln t g 2 x
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. R x = x 2 + 2 x - 1
Use a definição de continuidade e propriedades dos limites para demonstrar que a função é contínua em um dado número a . f x = x 2 + 7 - x , em a = 4 .
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. F x = s e n - 1 ( x 2 - 1 )