UFF, Niterói - Campus da Praia Vermelha, Cálculo IA, P1 - 2022.2, Questão 2b
Responda as seguintes perguntas (justifique suas respostas):
- Será que toda função que é contínua também é diferenciável?
Passo 1
Eaee!!! Belezinha? Seguinte... a questão nos faz uma pergunta um pouquinho filosófica haha
E aí... será que toda função que é contínua também é diferenciável?
A gente sabe que para uma função ser diferenciável, ela tem que ser contínua... mas o contrário também é verdade?
Já vou respondendo logo: Não necessariamente.
Quer saber o porquê? Então bora junto!!
😉
Passo 2
Então... Para uma função ser diferenciável em um ponto, ela deve ter uma taxa de variação bem definida nesse ponto, ou seja, sua derivada deve existir naquele ponto.
No entanto, a continuidade de uma função apenas garante que não há descontinuidades abruptas nos valores da função, mas não necessariamente implica que a derivada exista em todos os pontos.
Existem casos em que uma função pode ser contínua em um ponto, mas a sua derivada pode não existir naquele ponto devido a uma cuspide, um "pico" ou uma "reentrância" na curva da função.
Um exemplo comum é a função valor absoluto ().
A função é contínua em , mas não é diferenciável nesse ponto porque a derivada não é única devido à mudança de inclina��ão da curva. Veja:
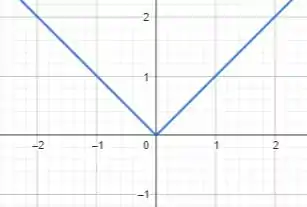
Em resumo, a continuidade é uma condição mais fraca do que a diferenciabilidade.
Todas as funções diferenciáveis são contínuas, mas nem todas as funções contínuas são diferenciáveis.
A diferenciabilidade de uma função depende da sua suavidade e da existência de uma taxa de variação bem definida em cada ponto do seu domínio.
Entendeu direitinho? Responde aee ;)
Resposta
Não