Sabe-se que e está definida em . Todas as afirmações abaixo são falsas. Desenhe um contra-exemplo para cada uma delas.
a) para
b)
c) é positivo
Passo 1
Faaala galera, nesse exercício vamos argumentar sobre descontinuidade de funções num ponto e como isso afeta o nosso limite.
Vamos de letra a:
para
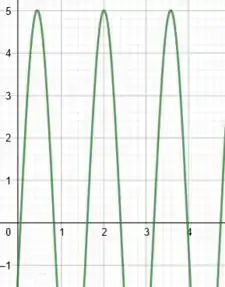
Ao observamos que , sabemos que a nossa função é positiva e tende a 5 quando se aproxima do valor 2 tanto pela esquerda quando pela direita. Ou seja, valores muitíssimo próximos de 2 realmente vão caracterizar , mas o intervalo (1,3) também possui uma certa distância de x = 2 e, portanto, pode ocorrer ainda que nos seus extremos haja .
Exemplo:
Passo 2
Vamos discutir agora sobre continuidade
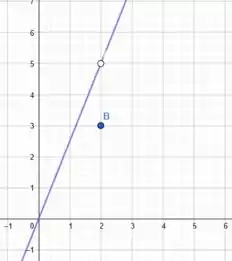
Letra b:
Simples, embora esteja definida em isso não significa que implica em visto que a função pode não ser continua nesse ponto, de forma que ela assume um valor diferente de 5 nele.
Letra c:
Ora, podemos estender o que vimos na letra b para o seguinte:
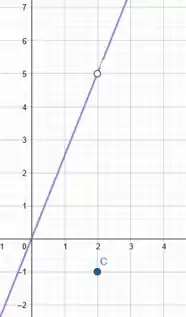
E é isso pessoal, finalizamos 😊
Resposta
Ei, a resposta está no passo a passo :)