Seja uma função contínua. Dois pontos de seu gráfico estão marcados no plano cartesiano abaixo. É possível garantir que existe tal que Justifique.
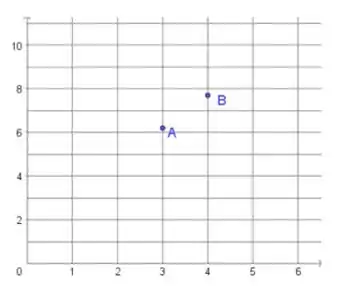
Atenção: As intersecções da malha são os pontos de coordenadas naturais. O ponto está ligeiramente acima do ponto e o ponto está ligeiramente abaixo do ponto .
Passo 1
Oieeee, tudo certinho por aí?
Essa questão é bem interessante. É falado que temos uma função contínua (essa informação é super importante aqui haha), mas não é dada a lei de formação de . É apenas mostrado dois pontos que pertencem a , e , no plano cartesiano.
A questão nos pergunta se é possível garantir que existe algum que vale .
Ou seja, basicamente o enunciado nos pergunta se podemos garantir que a curva possui pelo menos um ponto de intersecção com a curva . Beleza até aqui?

Bom, parece um pouco complicado porque temos pouquíssimas informações sobre . Mas, a ideia é utilizar o teorema de Bolzano.
Segundo ele, se é uma função contínua em um intervalo fechado , e é um número entre e , então com certeza existe algum tal que .
Vem comigo que vamos ver direitinho como aplicar essa ideia aqui!
Passo 2
Nessa questão temos apenas dois pontos da função : e .
Mas, sabemos que é contínua em , que é a nossa hipótese pra poder utilizar o teorema de Bolzano.
Ué, mas esse intervalo num tá aberto? No teorema o intervalo precisa ser fechado!
Então, esse intervalo de fato está aberto, mas se caminharmos um “cabelinho de sapo” pra dentro desse intervalo, teremos um intervalo fechado que ainda satisfaz as nossas condições. Tranquilo?

Continuando, sabemos que:
está um pouquinho acima de . E, está um pouquinho abaixo de .
Ou seja, temos um ponto que está um pouquinho acima da reta e outro que está um pouquinho abaixo da mesma reta. Dando um zoom na imagem, o que temos é isso daqui:
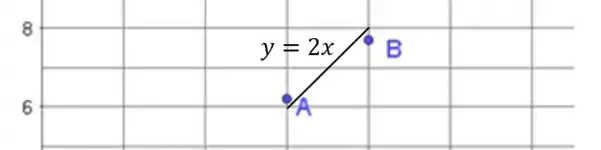
Ou seja, pensando no nosso teorema de Bolzano, é qualquer ponto pertencente a reta no intervalo . E, conseguimos garantir que:
Assim, temos todas as condições pra chegar na conclusão do teorema: é contínua no intervalo fechado, e é um número entre e . Portanto, com certeza existe um , tal que:
Massaaa! Tem uma forma bem intuitiva de perceber isso também. Basta perceber que fisicamente não temos como traçar nenhuma curva contínua que saia do ponto e chegue no ponto sem passar pela reta preta na imagem (.
Eaí, conseguiram entender bem direitinho a solução?
É isso aí então, muito obrigado pela atenção gente! Até a próxima 😊
Resposta
Resposta no texto.