USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 2.3
Seja f : R → R a função dada por f(x) = { , se ∈ Q; , se ∈ R \ Q.
O conjunto descontinuidades de f é: a. ∅; b. Q; c. R \ Q; d. R \ {0}; e. R.
Passo 1
Eaew, belezinha?
Temos que encontrar qual é o conjunto descontinuidade da função, tal que
Seja f : R → R a função dada por f(x) = { , se ∈ Q; , se ∈ R \ Q.
Temos que esse conjunto é aquele para o qual os limites laterais não existem ou não coincidem. Então vamos lá!
Passo 2
Olhando para a função, temos que se x for real os limites laterais não vão coincidir, pois as retas e não coincidem. Entretanto, essas retas irão coincidir quando x tender a zero, tanto pela esquerda, quanto pela direita, como vemos no gráfico abaixo:
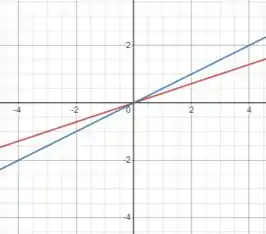
Então, podemos dizer que o conjunto descontinuidade da função são todos os reais, exceto o zero. Que corresponde ao item d. R \ {0}.
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
d. R \ {0}.