Seja a função definida por:
Determine o domínio de , esboce seu gráfico e determine sua imagem, .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função que tem diferentes formatos dependendo do intervalo em que ela se encontra:
E ele pediu pra gente encontrar o domínio e a imagem dela, além de esboçar seu gráfico. Tá bom, mas o que é domínio e imagem mesmo?
Bom, o domínio de uma função é o conjunto de todos os valores possíveis que a variável independente da função pode assumir. E quem é a variável independente? No nosso caso, como temos uma – uma função que depende de – a nossa variável independente é o .
Beleza, e a imagem da função? Enquanto o domínio tá relacionado com a variável independente, a imagem tá associada com a variável dependente. Ou seja, são todos os valores que a variável dependente irá assumir. Tranquilo, então o tá relacionado ao domínio e o à imagem.
Agora como é que eu faço pra encontrar esses valores que pode ou não assumir na função e garantir sua existência? Vamos analisar nossa função para descobrir.
Passo 2
Os valores que não pode assumir na função são as chamadas restrições. O domínio nem sempre vai ser um conjunto completo, muitas vezes, a variável independente não poderá assumir alguns valores específicos. Mas quais seriam esses valores?
No nosso caso, temos a função:
Isso me diz que quando é menor que , ; quando tá entre e , ; e quando é maior do , . Então, a pode assumir essas três formas e nós temos que avaliar em cada intervalo como ela se comporta.
Quando , nossa é uma reta crescente:
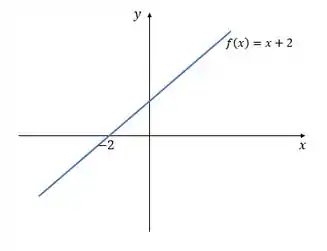
Ela não chega a cortar o eixo em , porque o nosso intervalo só vai até ali nesse caso. O esboço é só pra gente perceber que essa função não tem restrições, porque ela pode ir de até e pode assumir qualquer valor.
Passo 3
Agora analisando a segunda parte da função, quando , temos:
Olhando pra essa função a gente percebe que se trata de um polinômio, que nada mais é do uma soma de potência naturais de com coeficientes constantes. Nesse caso, o nosso polinômio é de segundo grau, mas não importa o grau, o que importa é que o domínio de qualquer polinômio é . Isso, porque o não vai ter nenhuma restrição, ele pode assumir qualquer valor e nós podemos visualizar isso olhando o gráfico:
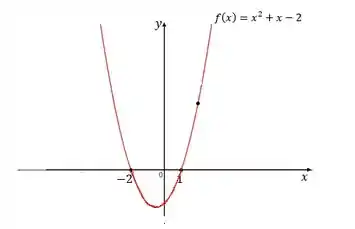
Pra gente, nesse caso, só interessa a parte de baixo da curva, que vai de a , onde tá o intervalo da nossa função. Mas a gente percebe que pra qualquer valor, ela estaria definida e por isso o domínio é .
Passo 4
Agora analisando a última parte da nossa função, quando , temos:
Que é uma função constante. Como ela independe do valor de , o nosso domínio continuaria em . E, começando de , o gráfico seria isso aqui:
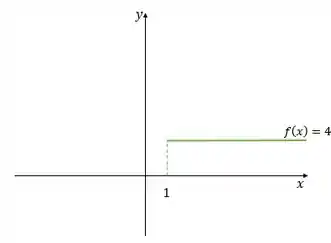
Mas observe que ele diz , então o ponto não está definido. Isso vai ficar mais claro quando a gente juntar os três gráficos, afinal de contas eles definem uma única função .
Passo 5
Juntado tudo, nós temos:
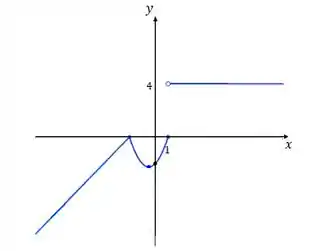
Nós vimos que o nosso domínio está em . Então,
Agora, lembra que no passo nós falamos que a imagem está relacionada aos valores que irá assumir? Olhando para o gráfico, a gente consegue ter uma ideia dessa valores, baseados nos intervalos da função.
A gente percebe que nossa função é contínua de até , e aí . Depois, quando a parábola termina no gráfico da figura acima, ela passa a ser , para . Traduzindo isso matematicamente, a nossa imagem é:
Outra forma de descrever é usando o símbolo de união entre os intervalos:
Prontinho, encerramos o exercício. Valeu, galera! 😉