Seja a função definida por
d) é contínua no intervalo fechado ? Justifique.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função definida por partes, onde ela apresenta uma lei de formação diferente pra cada intervalo considerado, e nós precisamos verificar se ela contínua no intervalo fechado .
Dizemos que uma função é contínua em um intervalo fechado , se as seguintes condições são satisfeitas:
a) é contínua em
b) é contínua a direita em , isto é,
c) é contínua à esquerda em , isto é,
Vamos analisar cada intervalo e verificar a lei de formação da função naquele intervalo, e calcular os limites para ver se a função atende as condições.
Vamos lá!
Passo 2
A primeira condição a ser satisfeita é de que seja contínua no intervalo aberto . Isso acontece quando é contínua em todos os pontos desse intervalo, o que acontece na nossa função, a gente pode perceber observando o intervalo no gráfico:
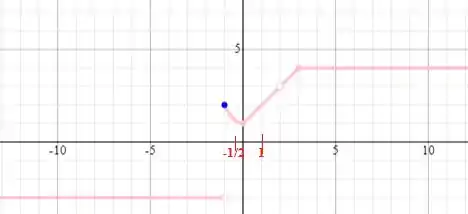
Testando a continuidade à direita, em , temos:
Calculando , temos:
Então, .
Agora testando a continuidade à esquerda, temos:
E . Logo, .
Como as três condições são satisfeitas, podemos dizer que é contínua em .
Valeu, galera! Até a próxima! 😉