UFF, Sem Campus, Cálculo IIB, P1 - Prof. Jorge Delgado - 2023 - Verão, Questão 1
Seja
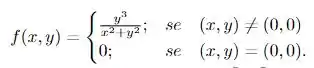
responda justificando.
é contínua em ?
possui derivadas parciais em ? Caso afirmativo calcule-as.
é diferenciável em ?
Passo 1
Eaew, tudo certinho contigo?
O enunciado nos deu a seguinte função
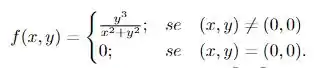
precisamos então avaliar as três alternativas, primeiro, a função é contínua em ? Segundo, a função possui derivada parciais em , e por último a função é diferenciável em ? Analisar a continuidade está relacionado a verificar a seguinte igualdade
para verificar a existência das derivadas parciais vamos calcular cada uma delas individualmente pela definição
e
E, finalmente, a diferenciabilidade pode ser analisada através das condições
A função deve ser contínua no ponto!
As derivadas parciais devem existir no ponto!
As derivadas parciais devem ser contínuas!
Vamos fazer tudo isso e verificar a diferenciabilidade de nossa função! Bora lá!
Passo 2
Primeiro, vamos calcular o limite da função, temos que
portanto, é uma indeterminação, vamos reescrever um pouco então o nosso limite! Podemos separá-lo da seguinte forma
Aqui, podemos garantir que
Mas o outro limite ainda é indeterminado! Note no entanto, que podemos garantir que
ou seja, temos que
e, portanto, o segundo limite é finito, e existe neste intervalo, desta forma, podemos garantir que
Como a função em é nula! A função é contínua nesse ponto! Bora para a próxima alternativa!
Passo 3
Usando a definição da função podemos então calcular as derivadas parciais em como
e
simplificando as expressões temos diretamente que
e
Essas são as derivadas parciais em , portanto, ambas existem! Maravilha! As duas primeiras condições da diferenciabilidade são válidas, mas será que a última é? Vamos verificar!
Passo 4
Para fazer essa verificação vamos partir do seguinte limite
usando a definição da função temos que
para verificar se o limite existe, vamos calculá-lo através de diferentes caminhos, se tomarmos o caminho em que , temos que o limite toma a forma
mas, e se tentarmos outro caminho, como por exemplo, , temos que
o surge pois temos o módulo dividindo, sendo assim, a razão carrega um sinal que não sabemos com certeza, pois pode ser negativo! Isso não importa, pois o limite é diferente se seguirmos por este caminho, desta forma nossas derivadas parciais não são contínuas! E, a nossa função não é diferenciável na origem! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
A função é contínua.
A função não é diferenciável.