UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Limites e Continuidade, Questão 5.4
Qual a semelhança entre o gráfico de
E o pato?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente verificar o que o gráfico da função tem em comum com o pato hahaha.
Bom, vamos montar o gráfico dessa função que é definida por partes e ver se a gente descobre o que isso tem a ver com um pato.
Vamos lá!
Passo 2
Nós temos uma função que é definida por partes, . Repare que ela tem uma lei de formação quando é maior ou igual a e outra lei de formação quando é menor do que .
Para , temos , que representa o gráfico de uma reta deslocada em uma unidade para para cima:
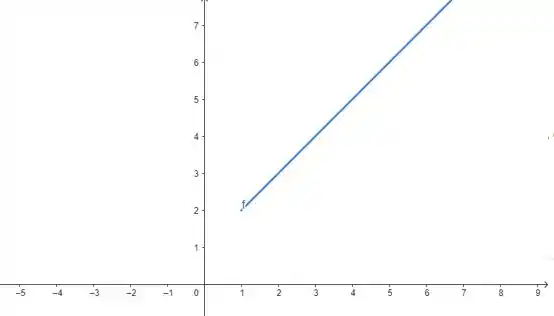
Repare que ela começa em , por causa da condição .
Passo 3
Agora quando , temos , que também representa o gráfico de uma reta só que expandida por um fator . Assim:
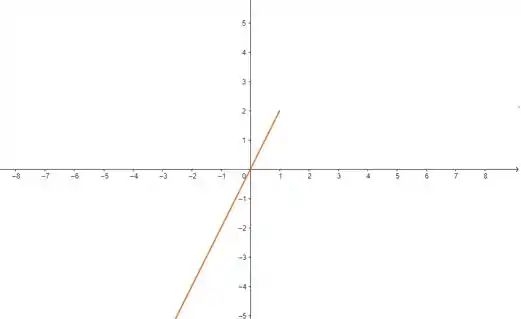
Como , repare que ela vem de até .
Juntando as duas, temos o gráfico de
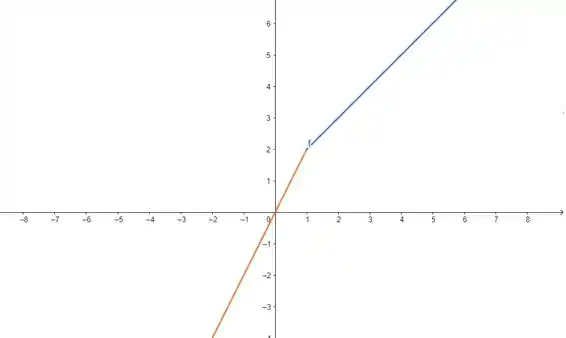
E o que isso tem a ver com um pato? Bom, o que nos parece é que o professor pode pode ter se referido ao bico que a função faz em . Dessa forma, a função é contínua no ponto, mas não é diferenciável, por isso não existe (como vimos na questão 5.3b).
Valeu, galera! Até a próxima! 😉