14) Verifique se a função dada é contínua nos pontos indicados. Justifique a resposta.
para , onde = maior inteiro que não supera . Pontos x = 0 e x = 1.(Sugestão: esboce o gráfico de )
Passo 1
Eaí galerinhaa, todos preparados para fazer um gráfico matador?
Quase sempre que a questão nos dá uma sugestão, é uma boa segui-la, até porque quem avisa amigo é né? Rs.
Sendo assim, vamos desenhar o gráfico dessa função tendo atenção principalmente à esse piso de . Quando por exemplo, então .
Passo 2
Desenhando o gráfico, temos:
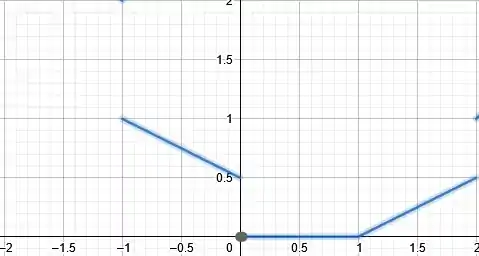
Passo 3
Pelo gráfico dá para perceber que a função é descontínua em , pois:
De forma bem parecida, mas agora em temos o resultado contrário, pois:
Resposta
é descontínua
é contínua