Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 451234567891011121314151617181920212223242526272829303132333435363738394041424344464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 3: Considere a região espacial

U = x ,   y ,   z ∈ R 3   |     z 2 ≤ x 2 + y 2 ,   x 2 + y 2 + z 2 ≤ 4 ,   x ≥ 0 ,   y ≥ 0 ,   z ≥ 0

Sabendo que o volume de U é

V o l U = 2 π 2 3

Calcule a coordenada z - do centroide de U .

Passo 1

Bem, se um problema nos pediu centroide, então o que precisamos fazer imediatamente é escrever a equação que nos dá o centroide para uma coordenada, no caso a coordenada z ...

z - = 1 V o l U ⋅ ∭ U   z   d V

No caso, o nosso problema já nos ofereceu o volume de U , nos restando somente que encontremos essa integral tripla, aí. Vamos nessa?

Passo 2

Ok! Para resolver a integral, precisamos descrever a região U , certo? Mas quem é essa região?

Bem, pelo enunciado, essa região é formada por essas desigualdades aqui:

U = x ,   y ,   z ∈ R 3   |     z 2 ≤ x 2 + y 2 ,   x 2 + y 2 + z 2 ≤ 4 ,   x ≥ 0 ,   y ≥ 0 ,   z ≥ 0

Onde a primeira desigualdade no indica que estamos trabalhando com uma região pra fora do cone...

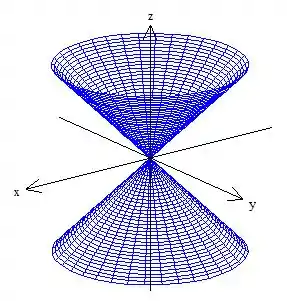
A segunda desigualdade, x 2 + y 2 + z 2 ≤ 4 , nos indica que estamos trabalhando dentro da esfera de raio 2 ...

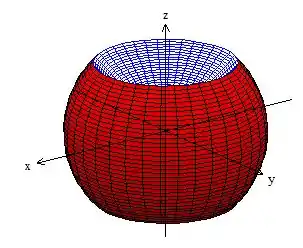
Já as três últimas desigualdades, x ≥ 0 ,   y ≥ 0   e   z ≥ 0 , nos indica apenas que estamos trabalhando com um sólido no primeiro octante. Assim, ganhamos a visualização do nosso sólido U :

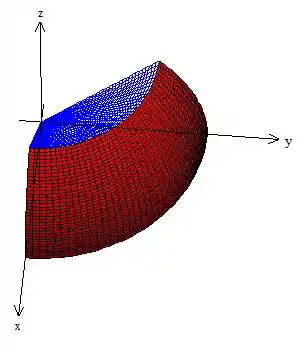
Passo 3

Bem, se estamos trabalhando com uma região no interior de uma esfera, talvez facilite um pouco se trabalharmos com as coordenadas esféricas, onde usamos:

x = ρ sin ⁡ φ cos ⁡ θ

y = ρ sin ⁡ φ sin ⁡ θ

z = ρ cos ⁡ φ

Não se pode esquecer de que o Jacobiano dessa mudança vale...

J = ρ 2 sin ⁡ φ

Ok, mas agora, com essa mudança, precisamos encontrar onde essas novas variáveis, variam para descrevermos o nosso sólido U . Bora?

Passo 4

Podemos entender onde essas novas variáveis variam dentro da nossa região por comparação entre o nosso sólido e o diagrama de variação das variáveis em coordenadas esféricas:

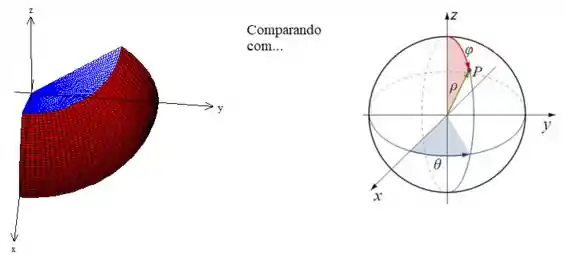
Veja que imediatamente conseguimos perceber que o θ dá um quarto do volta, saindo de 0 e indo até 90 ° ...

0 ≤ θ ≤ π 2

Já o ρ , varia de 0 e vai até o raio máximo que é a esfera com raio R = 2 ...

0 ≤ ρ ≤ 2

Enquanto ao φ , bem veja que ele é o cara que começa a rodar, quando ele entra pelo cone, e sai em no chão z = 0 ...

C o n e ≤ φ ≤ c h ã o   z = 0

Como no cone, sabemos que...

z 2 = x 2 + y 2                   →                 t r o c a n d o   p e l a s   c o o r d e n a d a s   e s f é r i c a s                 →

ρ 2 cos 2 ⁡ φ = ρ 2 sin 2 ⁡ φ cos 2 ⁡ θ + ρ 2 sin 2 ⁡ φ sin 2 ⁡ θ       →

ρ 2 cos 2 ⁡ φ = ρ 2 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ       →

cos 2 ⁡ φ = sin 2 ⁡ φ       →               cos ⁡ φ = sin ⁡ φ                 →

tan ⁡ φ = 1               e n t ã o                 φ = 45 ° = π 4

Logo

π 4 ≤ φ ≤ c h ã o   z = 0

No chão z = 0 ...

z = ρ cos ⁡ φ = 0           →           cos ⁡ φ = 0                   →

π 2

Então...

π 4 ≤ φ ≤ π 2

Passo 5

Com essas variações...

0 ≤ θ ≤ π 2

0 ≤ ρ ≤ 2

π 4 ≤ φ ≤ π 2

Podemos voltar para a integral...

∭ U   z   d V

E substituir, não se esquecendo de trocar z pelas coordenadas esféricas e multiplica-lo pelo Jacobiano...

∭ U   z   d V = ∫ 0 π 2 ∫ 0 2 ∫ π 4 π 2 ρ cos ⁡ φ ⋅ J   d φ d ρ d θ =

∫ 0 π 2 ∫ 0 2 ∫ π 4 π 2 ρ cos ⁡ φ ⋅ ρ 2 sin ⁡ φ   d φ d ρ d θ =

∫ 0 π 2 ∫ 0 2 ∫ π 4 π 2 ρ 3 cos ⁡ φ   sin ⁡ φ   d φ d ρ d θ

Integrando com relação a φ , lembrando que cos ⁡ φ   sin ⁡ φ = sin ⁡ 2 φ 2 ...

∫ 0 π 2 ∫ 0 2 ρ 3 ∫ π 4 π 2 sin ⁡ 2 φ 2   d φ d ρ d θ = ∫ 0 π 2 ∫ 0 2 ρ 3 - cos ⁡ 2 φ 4 π 4 π 2 d ρ d θ =

∫ 0 π 2 ∫ 0 2 ρ 3 - cos ⁡ π 4 - - cos ⁡ π 2 4 d ρ d θ =

∫ 0 π 2 ∫ 0 2 ρ 3 1 4 - - 0 4 d ρ d θ = 1 4 ∫ 0 π 2 ∫ 0 2 ρ 3 d ρ d θ

Integrando agora com relação à ρ ...

1 4 ∫ 0 π 2 ∫ 0 2 ρ 3 d ρ d θ = 1 4 ∫ 0 π 2 ρ 4 4 0 2 d θ =

1 4 ∫ 0 π 2 2 4 4 d θ = 16 16 ∫ 0 π 2 d θ =

π 2

Passo 6

MAS CALMA JOVEM!!! Ainda não acabamos não! Lembre-se que queremos encontrar a coordenada z do centroide, ou seja:

z - = 1 V o l U ⋅ ∭ U   z   d V

Substituindo tudo...

z - = 1 2 π 2 3 ⋅ π 2 = 3 2 π 2 ⋅ π 2 =

3 4 2 ⋅ 2 2 = 3 2 8

Resposta

3 2 8

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ