- Calcule os limites:
Passo 1
- Oi, galerinha! Tudo bom? Aqui temos um limite tendendo a infinito para resolver!
- Na letra b, quando substituímos x=1, encontramos uma indeterminação do tipo ,
A primeira coisa que faremos para tentar resolver esse limite é substituir na função e descobrir o que dá:
Repara que caímos em uma indeterminação do tipo .
Agora vamos tentar resolver esse limite!
Passo 2
Galera, quando tiver uma indeterminação deste tipo, a primeira coisa a fazermos é colocar o em evidência. Fica assim:
Repara que agora podemos cortar o ,
Por fim, vamos substituir o na função. Lembrando que uma costante dividida por um número muito grande tenderá a zero. Logo,
Agora vamos para letra b!
Passo 3
Para resolver essa indeterminação, temos que escrever esses polinômios. Pra isso, vamos precisar fatorar.
Vamos começar pelo denominador que é um polinômio de segundo grau. Para quem lembra, podemos reescrever um polinômio de segundo grau como um produto da seguinte forma:
Onde, e são as raízes da equação.
Vamos achar as raízes do polinômio do denominador, usando Bhaskara:
Logo as raízes são,
Uma vez que sabemos as raízes, podemos reescrever nosso denominador assim,
Então nosso limite fica assim,
Agora vamos mexer no nosso numerador!
Pessoal, a ideia aqui é encontrarmos um termo que anule o , para que não zere embaixo e conseguirmos determinar o nosso limite.
Passo 2
Para transformar um polinômio de terceiro grau em um produto polinômios, vamos usar Briot-Ruffini para a seguinte divisão, pois queremos que apareça um termo :
Para quem não lembra, primeiro a gente arma o quadro!
Escreva num quadro, como abaixo, os coeficientes do polinômio que se quer dividir alinhados do lado direito superior. A raiz do polinômio que dividimos deve estar do lado esquerdo superior. Já o primeiro coeficiente, do maior grau do polinômio, fica do lado direito inferior, logo abaixo de onde o escreveu em cima:

OBS.: Repare que colocamos um ali ocupando o espaço do grau . Para qualquer grau entre o grau máximo e o grau que tenha coeficiente nulo no polinômio, você precisa sempre escrever um no lugar do seu coeficiente.
Agora, multiplique a raiz pelo primeiro coeficiente, que você reescreveu embaixo ainda, e some-o com o próximo coeficiente (nesse caso, ). Escreva o resultado embaixo do segundo coeficiente, fica assim:
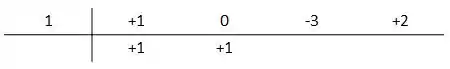
A ideia é repetir isso até chegarmos na última coluna,
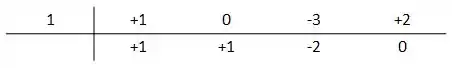
Escreva o resultado com os coeficientes ordenados, sendo o primeiro que aparece na direita inferior aquele que acompanha elevado a e assim por diante até o penúltimo, que será o termo independente de , uma constante! O último termo é o resto da divisão:
Agora vamos voltar para o nosso limite!
Passo 3
Agora que já fatoramos os polinômios do numerador e denominador, podemos escrever o nosso limite assim:
Simplificando e calculando o limite, ficamos com
Prontinho!
Resposta
- 0