![]()
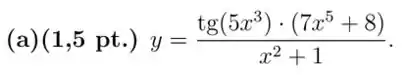
Passo 1
Temos um quociente aí. Vamos de Regra do Quociente!
Passo 2
Agora, falta calcular o termo . Pra ele, vamos usar a Regra do Produto:
Usamos a Regra da Cadeia na derivada da tangente:
Passo 3
Logo, teremos o seguinte:
Portanto,
![]()
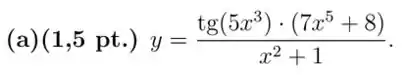
Temos um quociente aí. Vamos de Regra do Quociente!
Agora, falta calcular o termo . Pra ele, vamos usar a Regra do Produto:
Usamos a Regra da Cadeia na derivada da tangente:
Logo, teremos o seguinte:
Portanto,