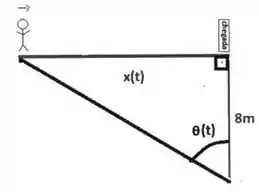
Uma câmera filma o atleta em sua corrida até a linha de chegada. A distância entre o atleta e a chegada é , a distância entre a câmera e a linha de chegada vale e, para manter o foco no atleta, a câmera faz com a linha de chegada o ângulo , conforme a figura. No instante , o atleta cruza a linha de chegada e a velocidade angular da câmera é
Argumente que
Com o auxílio da regra da cadeia, calcule a derivada
Determine a velocidade do atleta quando ele cruza a linha de chegada.
Passo 1
Falaaaa, blz???? Bora lá começar essa provinha de cálculo 1.
Bom, vamos olhar para cada alternativa separadamente e ir argumentando uma por uma, começando com a letra a.
Argumente que
Para essa afirmação, vamos lembrar do conceito de tangente. Dizemos que a tangente de um ângulo será o lado oposto ao ângulo sobre o adjacente, ou seja, olhando para figura, já fica claro qual a tangente do ângulo será
Passo 2
Bora agora olhar a letra
Com o auxílio da regra da cadeia, calcule a derivada
Bom, como a própria letra diz, usaremos a regra da cadeira, vamos lembrar que regra é essa??
Se temos uma função dada pela composição de funções, dizemos que:
Essa é a tal da regra da cadeia, agora basta usarmos ela nas funções do enunciado.
Vamos tomar
Ou seja, temos:
Como foi dito, pela regra, temos:
Porém, vale lembrar que ou seja:
Assim terminamos com a letra b, bora ver a última
Passo 3
Olhando a letra C
Determine a velocidade do atleta quando ele cruza a linha de chegada.
Bom, para essa letra, vamos lembrar que:
Ou seja, a velocidade é dada pela derivada da posição em relação ao tempo.
A informação do enunciado é que o atleta cruza a linha de chegada no tempo , ou seja, o que a letra nos pede é .
Usando a relação citada, o que nós queremos achar é
Lembrando que:
Derivando e usando o valor achado na última letra:
Agora, como foi dito, queremos analisar essa equação em , ou seja:
Primeiro, vamos lembrar do enunciado que:
Além disso, temos que , ou seja:
Porém, vamos analisar que , pois o ângulo formado entre o atleta e a linha de chegada, quando ele tá na linha de chegada será zero, além disso temos que , ou seja:
Assim terminamos o primeiro probleminha dessa prova, bora para o próximo?
Resposta
Tangente é lado oposto sobre adjacente, olhando para figura fica evidente que