Determine a derivada da função abaixo:
Passo 1
Pela regra da cadeia, a derivada do primeiro termo é
Passo 2
A derivada de também será calculada usando regra da cadeia:
Precisamos de . Lembrando que
E
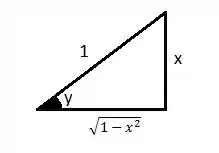E a partir do triângulo abaixo
Concluímos que
Assim, descobrimos que
Passo 3
Agora juntando as duas derivadas que calculamos teremos
Resposta
Exercícios de Livros Relacionados
Encontre a derivada da função.y = ((x^2 + 1)/(x^2 - 1))^3
Encontre a derivada da função.(d)/(d x) 2^(sen ( pi x ))
Encontre a derivada da função. y = r r 2 + 1
Encontre a derivada da função. G y = y - 1 4 y 2 + 2 y 5
Encontre a primeira e a segunda derivadas da função. y = e α x β x