Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra da Cadeia

Ver Teoria
Exercício 135123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Determine a derivada da função abaixo:

f x = s e n   x arctan ⁡ 2 x

Passo 1

Já que se trata de uma divisão, primeiro usaremos a regra do quociente:

f ' x = s e n   x ' arctan ⁡ 2 x - s e n   x ( arctan ⁡ 2 x ) ' arctan ⁡ 2 x 2

f ' x = cos ⁡ x arctan ⁡ 2 x - s e n   x ( arctan ⁡ 2 x ) ' arctan ⁡ 2 x 2

Passo 2

Agora bora calcular a derivada de arctan ⁡ 2 x pra depois jogar isso na expressão da derivada acima. É importante lembrar que:

f - 1 x ' = 1 f ' x

No caso que estamos estudando, isso pode ser escrito assim:

arctan' ⁡ x = 1 tan' ⁡ y

Sabemos que

arctan ⁡ x = y ↔ tan ⁡ y = x

tan ⁡ y em função de x , veja:

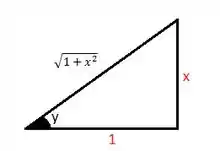
Como

t a n ' y = sec 2 ⁡ y

Olhando pro triangulo, vemos que

sec 2 ⁡ y = 1 cos 2 ⁡ y = 1 1 1 + x 2 2 = 1 + x 2

E, finalmente, já que

arctan' ⁡ x = 1 tan' ⁡ y

E

t a n ' y = sec 2 ⁡ y = 1 + x 2

Temos

arctan' ⁡ x = 1 1 + x 2

Passo 3

Acabou? Já posso botar tudo na expressão da derivada de f ? Naaaao

Faltou um pequeno detalhe. Queremos a r c t a n ' 2 x e não a r c t a n ' x , mas calma que é só um detalhe mesmo. Concorda que a r c t a n ' 2 x é uma composição de funções que pode ser derivada usando regra da cadeia? Então, já sabemos a derivada da função de fora, agora é só multiplicar pela derivada da de dentro e trocar tudo que for x por 2 x . Olha:

2 x ' = 2

Portanto teremos

arctan' ⁡ 2 x = 2 1 1 + ( 2 x ) 2 = 2 1 + ( 2 x ) 2 = 2 1 + 4 x 2

Passo 4

Voltando para

f ' x = cos ⁡ x arctan ⁡ 2 x - s e n   x ( arctan ⁡ 2 x ) ' arctan ⁡ 2 x 2

Vamos substituir a r c t a n ' 2 x por 2 1 + ( 2 x ) 2 e obter:

f ' x = cos ⁡ x arctan ⁡ 2 x - s e n   x 2 1 + 4 x 2 arctan ⁡ 2 x 2

f ' x = ( 1 + 4 x 2 ) cos ⁡ x arctan ⁡ 2 x - 2 s e n   x ( 1 + 4 x 2 ) arctan ⁡ 2 x 2

Resposta

f ' x = ( 1 + 4 x 2 ) cos ⁡ x arctan ⁡ 2 x - 2 s e n   x ( 1 + 4 x 2 ) arctan ⁡ 2 x 2

Exercícios de Livros Relacionados

Encontre a derivada da função.y = ((x^2 + 1)/(x^2 - 1))^3
Encontre a derivada da função.(d)/(d x) 2^(sen ( pi x ))
Encontre a derivada da função. y = r r 2 + 1
Encontre a derivada da função. G y = y - 1 4 y 2 + 2 y 5
Encontre a primeira e a segunda derivadas da função. y = e α x β x