UFABC – Cálculo 1 – Lista 2 – 12
Uma escada com 10m de comprimento está apoiada numa parede vertical. Seja o ângulo entre o topo da escala e a parede e a distância da base da escada até a parede. Se a base da escada escorregar para longe da parede, com que rapidez variará em relação a quando ?
Passo 1
E aí, gente!! Tudo bem? Vamos para mais um desafio?
A primeira coisa vai ser: BORA DESENHAR!!!
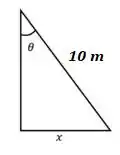
Aí está o desenho da escada de 10m apoiada verticalmente na parede à uma distância da parede até sua base e com ângulo entre a parede e a escada.
O enunciado tá pedindo pra gente avaliar A RAPIDEZ QUE VARIA EM RELAÇÃO A . Essa frase dá pra gente exatamente o que precisamos procurar, que é o
Ou seja, se a gente conseguir encontrar uma relação entre e , podemos ao final encontrar essa variação.
Passo 2
Olhando pro nosso desenho, vemos que o equivale ao cateto oposto do ângulo. E também conhecemos o valor de hipotenusa que é 10 m, certo?
Qual é a relação entre , e hipotenusa?
Passo 3
Tcharammmm, encontramos então uma equação que descreve em função de .
Agora, só precisamos derivar em função de para encontrar essa variação que foi pedida no enunciado.
Agora basta substituirmos o valor de e calcular que: