O movimento de uma mola sujeita a uma força de atrito é frequentemente modelado pelo produto de uma função exponencial e uma função seno. Suponha que a equação do movimento de um ponto sobre essa mole é:
em que s é medida em centímetros e t em segundos.
Encontre os instantes de tempo nos quais a partícula se encontra em repouso.
Passo 1
E aí, gente!! Tudo bem? Vamos para mais um desafio?
Primeiro vamos lembrar do entendimento físico do que é velocidade: variação da posição/deslocamento em relação ao tempo.
No nosso caso, o deslocamento foi dado pela equação , então, para calcular a velocidade precisamos fazer , que já fizemos na letra (a). O enunciado nos pede pra saber os instantes em que a partícula se encontra em repouso e sua respectiva posição. Para encontrar o tempo que a partícula está em repouso, temos que a velocidade precisa ser igual a zero, certo?
Passo 2
Assumindo a velocidade encontrada na letra (a):
Para estar em repouso, temos que ter:
Passo 3
Para encontrar os valores de encontro, precisamos plotar um gráfico e analisar.
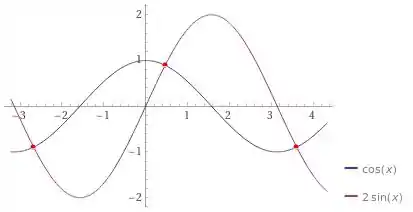
Observe que temos alguns pontos em específico e resolvendo essa igualdade via algum software matemático, podemos encontrar que