UFPA, Sem Campus, Cálculo II, Listas de Cálculo 1 - Profº Tiago Coelho - Lista de Exercícios 5, Questão 3
Questão 3. Considere um triângulo retângulo de catetos e e seja o ângulo adjacente a . Calcule e e aplique ao caso , .
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão temos um triangulo retângulo de catetos e e o ângulo adjacente a .
Nessa situação, queremos obter as derivadas parciais e e depois aplicar o ponto nos resultados.
Tem alguma ideia de como fazer isso? 😬
A primeira coisa que temos que fazer é escrever em função de e . Pra isso podemos usar algumas relações trigonométricas a partir do triangulo retângulo.
A partir daí podemos escrever um valor infinitesimal de em relação a um valor infinitesimal de e .
Compreendeu? Bora ver como é na prática 😉
Passo 2
Esboçando o triângulo retângulo, temos
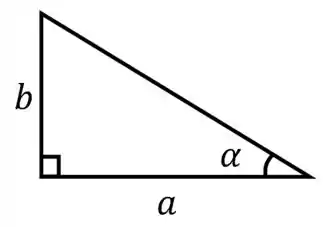
A partir desse triângulo, podemos usar as relações trigonométricas da tangente como
Assim, isolando , vamos obter
Portanto, podemos derivar em função de como pela regra da cadeia
Como , então
Tranquilo até aqui? 😁
Passo 3
Agora vamos derivar em relação a pelo mesmo método
Como
Por fim, aplicando o ponto nas derivadas, chegamos em
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
