C2) Sejam a função cujo gráfico está abaixo.
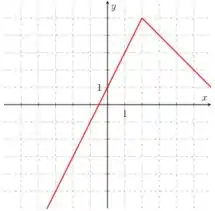
Determine , em que .
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!

Esse enunciado nos pede para encontrarmos . Mas o que isso significa?
é a derivada da função no ponto em que . Ou seja, o que devemos fazer é derivar e aplicarmos, quando necessário, o valor de
Vamos, então, avaliar . Perceba que dentro de temos aparecendo e precisamos descobri-lo para continuarmos os cálculos.
Para definirmos , precisamos observar o gráfico e considerar o seguinte: como precisamos encontrar a derivada no ponto , precisamos definir a reta que passa por . Essa reta nada mais é que .
Observando a reta, podemos definir dois pontos. Um ponto é e o outro é . Como conhecemos dois pontos da reta, podemos utilizar a equação geral da reta para defini-la:
A equação geral da reta é:
Vamos inserir os pontos que encontramos:
é o valor do coeficiente angular da reta. É o valor que acompanha em:
Agora precisamos definir . Como temos e um ponto da reta:
Portanto, a reta é:
Passo 2
Precisamos, agora, aplicar em :
Então calcularemos a derivada e esse é um caso clássico da regra da cadeia. Ok, mas quando usamos a regra da cadeia?
A regra da cadeia será utilizada sempre que tivermos uma função composta, que nada mais é do que uma função dentro de outra, ou seja um “aninhamento” de funções. Matematicamente, uma função composta é , onde e , e sua derivada é: .
Para o nosso caso:
Como queremos encontrar a derivada no ponto , vamos substituir :
Ufa! Terminamos!

Pra essa questão é isso pessoal! Bora pra mais uma?