Um silo tem a forma de uma pirâmide de base quadrada invertida, com uma altura de m e diagonal da base de m. O tanque se esvazia de um líquido não viscoso à taxa de . Com que velocidade se encontra o nível de líquido quando a altura dele estiver a m do fim?
Passo 1
Faaaala pessoal! Vamos extrair as informações necessárias para obter o volume do sólido e fazer a relação para obter o volume de líquido preenchido.
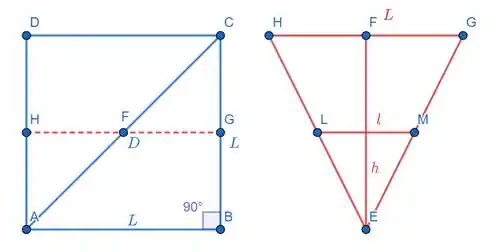
O quadrado é a base da pirâmide de diagonal . De , temos:
Passo 2
Agora, temos de extrair uma relação entre e , a fim de parametrizar o volume do líquido. O triângulo é uma seção transversal da pirâmide e está demarcado na representação da base. Da semelhança , temos:
Assim, o volume do líquido preenchido (pirâmide de base quadrada) é dado por:
Passo 3
Pensando na variação do volume no tempo, temos pela Regra da Cadeia:
O líquido escorre a vazão constante , da expressão acima quando , temos que:
Resposta
Assim, o nível do líquido desce () com velocidade .