Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 113123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 2: Considere a região E ⊂ R 3 limitada pelas superfícies regulares dadas pelas equações:

x - 1 2 + y 2 = 1 ,           z + 1 = x - 1 2 + y 2 ,     z = x ,

E a curva espacial regular C ⊂ R 3 interseção das superfícies regulares dadas pelas equações:

x - 1 2 + y 2 = 1 ,       z = x

Orientada de modo que a projeção ortogonal de C no plano x y tenha a orientação horária.

  1. Faça um esboço da fronteira de E e da curva C , indicando a orientação de C .
  2. Calcule a integral de linha.

∫ C   F d r

Do campo espacial F x ,   y ,   z = y 3 3 ,   e sin ⁡ y 2 ,   y x - 1 2 .

(Dica: Aplica o teorema de Stokes a uma superfície natural cujo bordo é C )

Passo 1

L e t r a   A )

Vamos desenhar a região desenhando cada superfície que a compõe primeiro:

x - 1 2 + y 2 = 1

Um cilindro de raio 1 e deslocado da origem:

z + 1 = x - 1 2 + y 2

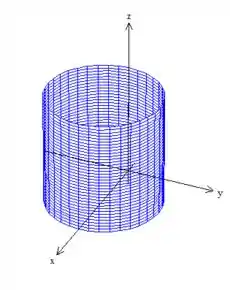
Um paraboloide como esse daqui: z = x 2 + y 2 , mas deslocado uma unidade em x e uma unidade pra baixo em z :

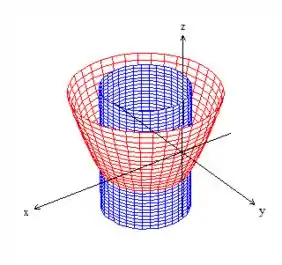
Por último, z = x é um plano:

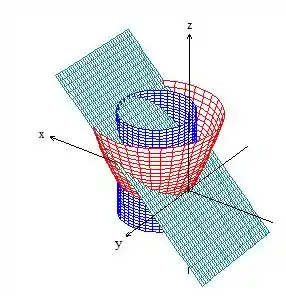
Colocando essas três superfícies juntas, percebendo que o cilindro e o paraboloide intercedem m z = 0 :

x - 1 2 + y 2 = 1 z + 1 = x - 1 2 + y 2   →         z = 0

Teremos...

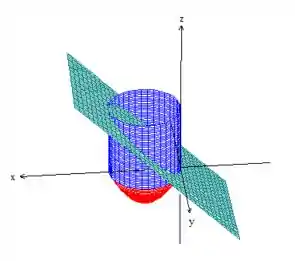
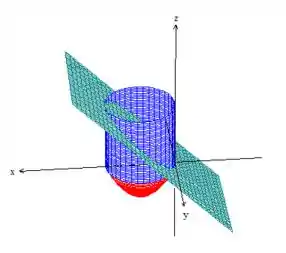
Yup! A região E : um cilindro com uma base de um paraboloide e um teto de passe planar ! A fronteira da curva C é apenas aquela curva elíptica da intersecção do plano com o cilindro!

Passo 2

Para calcular a integral de linha:

∫ C   F d r

Podemos usar, como na dica, o teorema de Stokes:

∫ C   F d r = ∬ S   r o t F → ⋅ n → d S

Agora, não podemos aplicar a dica sem antes averiguas as hipóteses do Teorema:

  • Temos que ter uma curva fechada C delimitando uma superfície S .
  • Precisamos de uma orientação positiva entre a curva e a superfície.
  • O campo F → não pode ter nenhuma singularidade.

Passo 3

Com relação ao primeiro quesito:

Ora, temos uma curva fechada C , agora quem pode ser a superfície que possui essa C como borda? Exatamente! O plano z = x que ajuda a formara a curva:

Passo 4

Com relação ao segundo quesito:

Precisamos de uma orientação positiva! Ora, a curva C gira como está na sua projeção: no sentido horário vista de cima, pela Regra da mão direita, precisamos que a superfície esteja orientada com o vetor normal para baixo!

Prontinho! Orientação concluída

Passo 5

Com relação ao último quesito:

Devemos verificar se o campo F → tem ou não singularidades onde estamos trabalhando:

F x ,   y ,   z = y 3 3 ,   e sin ⁡ y 2 ,   y x - 1 2

Por sorte tal campo não tem nenhum problema de definição!

Passo 6

Finalmente, após verificar as três hipóteses do teorema, podemos aplica-lo sem problemas:

∫ C   F d r = ∬ S   r o t F → ⋅ n → d S

Para calcular essa integral de superfície e matar o nosso problema utilizando a igualdade de Stokes, devemos:

  1. Parametrizar a superfície.
  2. Calcular o termo n → d S
  3. Calcular o rotacional e mudar os termos para os termos da parametrização.

Vamos nessa?

Passo 7

Poxa, estamos lidando com um plano z = x , então nada mais justo que parametrizarmos utilizando parametrização explícita, onde podemos encontrar todos os pontos σ do plano assim:

σ x ,   y = x ,   y ,   z x =

x ,   y ,   x

Onde x e y variam dentro do cilindro:

x - 1 2 + y 2 = 1

Passo 8

Para calcular o termo n →   d S , podemos fazer:

n → d S = N → d x d y

Onde

N → = - ∂ z ∂ x , - ∂ z ∂ y ,   1   →

N → = - 1,0 ,   1

Agora, perceba que esse vetor normal aí está apontado pra cima e o que queremos tem que estar apontado para baixo. Logo invertemos o seu sinal...

n → d S = 1,0 , -   1 d x d y

Passo 9

Por último, antes de retornar para a integral...

r o t F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

onde

F x ,   y ,   z = F 1 ,   F 2 ,   F 3 = y 3 3 ,   e sin ⁡ y 2 ,   y x - 1 2

Calculando as derivadas então...

r o t F → = x - 1 2 - 0 ,   0 - 2 y x - 1 ,   0 - y 2   →

r o t F → = x - 1 2 ,   - 2 y x - 1 ,   - y 2  

Como não tem nenhum z (único termo que muda com relação a parametrização) esse campo já é o campo em termos da parametrização σ :

r o t F → σ x ,   y = x - 1 2 ,   - 2 y x - 1 ,   - y 2

Passo 10

Finalmente aplicando na integral de superfície:

∬ S   r o t F → ⋅ n → d S = ∫     ∫ D   x - 1 2 ,   - 2 y x - 1 ,   - y 2 ⋅ 1,0 , -   1 d x d y =

∫     ∫ D   x - 1 2 + y 2   d x d y

Como estamos trabalhando no interior desse disco:

x - 1 2 + y 2 = 1

Podemos fazer uma mudança para coordenadas polares da seguinte forma:

x - 1 = r cos ⁡ θ

y = r sin ⁡ θ

J = r

Onde devido ao fato de cos 2 ⁡ θ + sin 2 ⁡ θ = 1 ...

x - 1 2 + y 2 = r 2

E perceba que para formar o disco inteiro, θ tem que estar dando uma volta completa enquanto r varia de 0 até 1 (raio máximo do cilindro).

Então...

∫     ∫ D   x - 1 2 + y 2   d x d y = ∫ 0 2 π ∫ 0 1 r 2 ⋅ r   d r d θ =

∫ 0 2 π ∫ 0 1 r 3   d r d θ = ∫ 0 2 π r 4 4 0 1 d θ =

1 4 ∫ 0 2 π d θ = 1 4 2 π =

π 2

Passo 11

π 2

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê