Avalie os limites abaixo e encontre o correspondente valor caso exista. Justifique suas respostas.
Passo 1
(a) Então pessoal, tem um monte de expressões complicadas ali, mas vamos olhar uma por uma com calma.
O primeiro limite que a gente quer resolver é esse aqui:
Logo de cara: dá pra simplesmente substituir com ? Olha o que ia acontecer:
Aparece um zero naquele denominador, então isso não vai dar certo. Temos que pensar em outro jeito.
Esse limite aí é um exemplo clássico em que a gente pode usar o teorema do sanduíche!
Esse teorema é muito útil quando você tem uma função limitada (que é o caso do cosseno, que varia só entre e ) multiplicada por uma função que vai pra zero (que é o caso do quando ).
Passo 2
A ideia é a seguinte, a gente vai achar duas funções bem simples, que tenham um limite fácil de calcular.
Uma delas vai sempre ser maior ou igual à nossa, e a outra vai ser sempre menor ou igual. A ideia é que essas duas formem um sanduíche com a função da questão.
A nossa função é essa aqui:
Vamos procurar uma função que seja sempre maior ou igual a essa. Bom, já que aquele cosseno ali sempre vai ser no máximo igual a , então essa função aqui:
Sempre é maior ou igual a . Ok, achamos o primeiro lado do sanduíche:
Passo 3
Agora é só pensar pela mesma lógica pra encontrar o outro lado do sanduíche! Vamos olhar nossa função de novo:
A gente já viu que o valor máximo é , que acontece quando o cosseno dá . E qual o outro extremo?
O valor mínimo acontece quando o cosseno dá ! Ou seja, essa função aqui:
É sempre menor ou igual à nossa função! Ótimo, nosso sanduíche está completo:
Dá uma olhada no gráfico pra entender isso melhor:
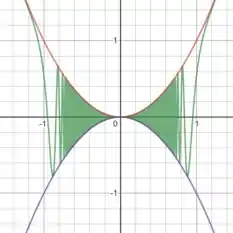
É um sanduíche perfeito!
Passo 4
Tá, e como você vai calcular o limite com essa relação? Bom, o teorema do sanduíche diz o seguinte, se você tem três funções seguindo essa regra aqui:
E os limites de e são iguais:
Então o limite de também é quando o tende a esse mesmo valor .
Esse é exatamente o nosso caso! Quando o nosso tende a zero, os limites das funções do nosso sanduíche são:
Nos dois casos é só substituir direto pra calcular o limite.
Então, pelo teorema do sanduíche (ah, na sua prova você pode escrever “teorema do confronto”, que é o nome mais correto hahaha):
Ok, o primeiro limite já foi.
Resposta
(a) .