UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 3b.
3. Calcule os seguintes limites (Não pode usar a regra de ):
b)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema, estamos interessados em calcular alguns limites, porém a única regra é que não podemos usar a regra de .
Entendeu?
A regra de nos ajuda muito quando temos uma indeterminação como resultado de um limite pelo método da substituição.
Porém existem alguns outros métodos que podemos aplicar a algumas analises matemáticas, com isso, vamos ter que analisar cada caso separadamente para ver qual é a melhor maneira de resolver o problema.
Sacou? Bora lá! 😁
Passo 2
O limite que temos que calcular é
Para facilitar nossa análise, vamos chamar de , e, portanto, e
Tirando a constante para fora do limite, vamos ter
Nesse caso podemos usar o teorema do confronto, mas antes vamos ter que fazer algumas análises trigonométricas.
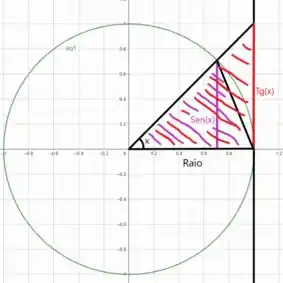
Vamos comparar algumas características desse círculo trigonométrico. Nele podemos ver que a área do triângulo roxo formado pela altura e pelo raio é menor que a área do setor circular com raio e que por sua vez é menor que a área em vermelho da , ou seja
Se a área de um triângulo é e a área de um setor circular é , então
Multiplicando por e simplificando...
Tudo certo até aqui? 👀
Passo 3
Agora, nessa inequação, vamos dividir tudo por
Como , então
Estamos interessados no inverso de então vamos inverter todos os lados. Lembrando que ao fazer isso, temos que inverter os sinais da inequação
E agora aplicando o limite em tudo, temos
Se e pelo método de substituição, então
Substituindo no nosso problema, temos
É isso! Essa resolução te ajudou? Responde Aí! ✌
