UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Limites e Continuidade, Questão 4.2
Mostre que a equação tem pelo menos três soluções reais.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente mostrar que aquele polinômio tem pelo menos uma solução dentro do conjunto dos números reais, quer dizer, ele tem pelo menos uma raiz real.
O Teorema de Bolzano nos garante, para uma função contínua, a existência de uma raiz na função, quando , se no intervalo .
Isso quer dizer que dentro de um intervalo existe um número que tem um correspondente , e esse nos fornece uma raiz quando o produto de e é negativo (menor do que zero). Calma, vamos dá uma olhadinha na representação do gráfico:
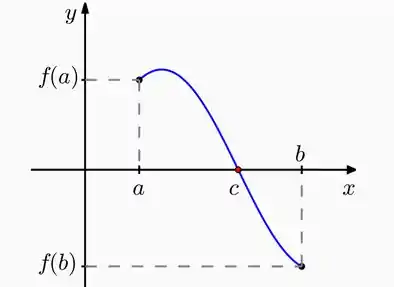
Repare que cruz o eixo quando . Observe que está dentro do intervalo e que é positivo e é negativo. Quando fazemos , temos um número negativo também. Poderia ser negativo e positivo, o produto também seria um número negativo. O importante é que quando ocorre essa mudança de sinal, a função passa pelo eixo e temos uma raiz ali.
Então, o que nós vamos fazer é chutar valores positivos e negativos para o a função (que por ser um polonômio já é uma função contínua) e verificar onde esse valores mudam de sinal () pra que possamos determinar a existência de uma raiz.
Vamos lá!
Passo 2
Vamos começar chutando na função :
Então, . Agora vamos chutar na função:
Logo, e temos uma raiz no intervalo .
Passo 3
Agora vamos fazer na função:
Então, . Agora vamos chutar na função:
Então, e temos:
Como não existe raiz nesse intervalo. Vamos continuar procurando.
Vamos fazer agora :
Fazendo , temos:
Logo, e temos uma raiz no intervalo .
Passo 4
Vamos fazer agora :
Fazendo , temos:
Logo, e temos uma raiz no intervalo .
Prontinho, galera! Até a próxima! ���
Resposta