UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Limites e Continuidade, Questão 3.6
O limite existe?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente verificar se o limite da função quando se aproxima muito de existe.
Como causa uma indeterminação na função, vamos verificar se o limite existe através dos limites laterais:
Se esses limites existirem e forem iguais, o limite existe.
Vamos lá!
Passo 2
Vamos analisar o comportamento da função quando se aproxima de zero pela esquerda:
Vamos atribuir alguns valores para próximos de pra ver o que acontece:
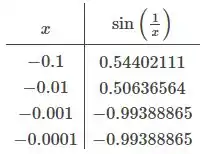
À medida que os valores de aproximam de , os valores da função se aproximam de . Portanto, o limite de à medida que se aproxima de pela esquerda é .
Agora considerando o valor crítico direito, , vamos ver como se comporta a função quando se aproxima de zero pela direita:
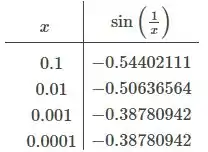
À medida que os valores de aproximam de , os valores da função se aproximam de . Portanto, o limite de à medida que se aproxima de pela direita é .
Como os limites laterais não são iguais, não existe.
Prontinho, galera! Até a próxima! 😉