Calcule os seguintes limites
(b)
Passo 1
Sumir com a indeterminação
Toda vez que vemos uma função seno ou cosseno num limite, pra não termos problema com o que tem dentro dela, é bom a gente reescrever o limite a fim de sumir com a indeterminação, caso tenha. Bora lá então. Se:
Então:
E se , então
Nosso limite ganha a seguinte cara:
Passo 2
Resolver por Teorema do Confronto
Opa, agora que minha função seno ficou “normal”, vamos ver se o teorema do confronto nos diz algo sobre esse limite. Vamos lembrar que:
Logo:
E aplicando o limite:
Sendo assim, vamos ter:
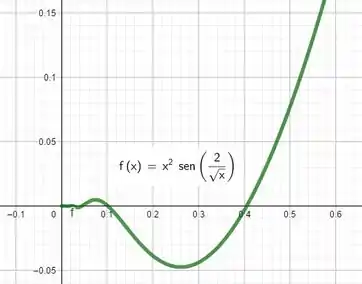
Graficamente, podemos ver que realmente quando , a função tende à e que ela está sempre entre as funções .
Ou ainda, pra ficar mais bonito ainda, podemos ver que no gráfico do limite original realmente o limite é .