UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Limites e Continuidade, Questão 4.5
Mostre que o conjunto
admite um maior e um menor elemento. Você consegue calcular estes valores?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente verificar se existem máximos e mínimos dentro do conjunto e verificar se a gente consegue calculá-los.
O teorema de Weierstrass (ou teorema dos Valores Extremos) nos diz que se é uma função contínua definida em um conjunto fechado e limitado , então tem valores extremos absolutos em .
Então, vamos avaliar o conjunto com base no teorema de Weierstrass. Vamos lá!
Passo 2
A primeira coisa é verificar se a nossa função é contínua no intervalo . Vamos olhar o gráfico da função:
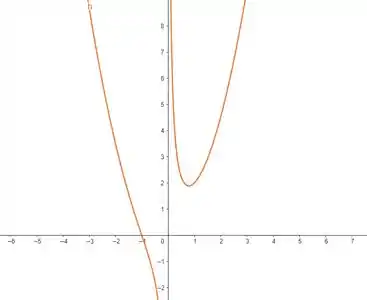
Repare que no intervalo , nossa função é contínua. E a função também está em um conjunto fechado, que é nosso intervalo, então ela atende a todos os requisitos do teorema de Weierstrass.
Sendo assim, podemos afirmar que existem valores e em , tais que é o valor mínimo de no intervalo, e o valor máximo de nesse mesmo intervalo. Assim,
Nós podemos encontrar e , derivando a função e igualando o resultado a zero.
Prontinho, galera! Até a próxima! 😉