A barra de comprimento e resistência está apoiada sobre o trilho fixo, indeformável e de resistência desprezível, conforme mostra a Figura. Os lados e são muito longos. O fio muito longo e retilíneo alinhado com o eixo conduz a corrente constante . Um agente externo exerce uma força de módulo sobre a barra, que a afasta do fio com velocidade constante no sentido positivo do eixo , de modo que .
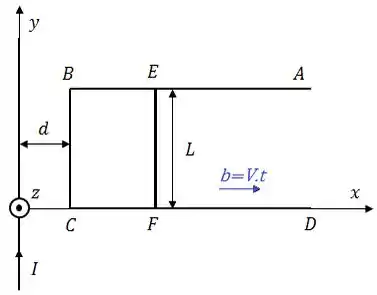
Determine o vetor campo magnético gerado pelo fio muito longo em um ponto arbitrário do semipleno .
Calcule o fluxo magnético através da espira em função dos dados fornecidos.
Calcule a corrente induzida na espira em função dos dados fornecidos e, justificando, indique seu sentido (horário ou anti-horário).
Passo 1
Determine o vetor campo magnético gerado pelo fio muito longo em um ponto arbitrário do semiplano .
O campo magnético é determinado através da lei de Ampère, dada por:
No caso do fio, a nossa amperiana será um círculo de raio , que envolve o fio de corrente . Assim, a lei de Ampère pode ser simplificada pra:
Mas como estamos interessados no campo magnético no semiplano , a distância do ponto em que estamos calculando o campo magnético ao fio será , logo:
De acordo com a regra da mão direita, orientando no sentido da corrente, o vetor campo magnético, no semiplano , será:
Passo 2
Calcule o fluxo magnético através da espira em função dos dados fornecidos.
Por definição, o fluxo magnético é dado por:
Como o campo magnético atravessa a espira perpendicular a ela, os vetores e serão paralelos, logo:
Onde:
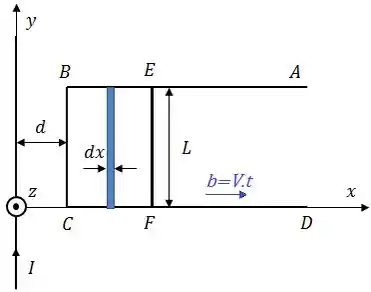
Logo:
Passo 3
Calcule a corrente induzida na espira em função dos dados fornecidos e, justificando, indique seu sentido (horário ou anti-horário).
Pra calcular a corrente induzida, primeiro vamos ter que calcular a induzida, que é determinada através de lei de Faraday:
A corrente será dada por:
Passo 4
O sentido da corrente é determinado pela lei de Lenz, que diz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Resumindo, o que ela diz é o seguinte:
Se o fluxo magnético estiver aumentando na espira, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Se o fluxo magnético estiver diminuindo na espira, o campo magnético induzido vai estar no mesmo sentido do campo magnético externo.
Como o fluxo magnético é dado por:
Logo:
Isso significa que o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Nesse caso, o campo magnético induzido estará saindo do plano da página. Para que isso ocorra, a corrente induzida deve estar no sentido anti-horário.
Resposta
A corrente induzida está no sentido anti-horário.