Lei de Lenz, Lei de Faraday, Forças e Torque sobre uma Espira
A barra condutora de comprimento e massa cai no campo gravitacional escorregando sem atrito sobre um fio condutor na forma de um ligado a um resistor de resistência , conforme a figura. O conjunto forma um circuito na vertical que se encontra na presença de um campo magnético uniforme na direção perpendicular ao plano do circuito.
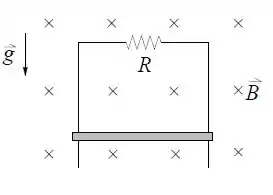
- Qual é o sentido da corrente induzida no circuito? Justifique.
- Calcule a f.e.m. induzida no circuito em termos do módulo da velocidade instantânea da barra na direção vertical.
- Determine a velocidade terminal da barra e a corrente que passa no circuito quando ela se encontra neste velocidade.
- Calcule a potência dissipada pelo sistema na situa do item (c) e mostre que ela é igual à potência fornecida ao sistema pelo campo gravitacional.
Passo 1
- Qual é o sentido da corrente induzida no circuito? Justifique.
- Calcule a f.e.m. induzida no circuito em termos do módulo da velocidade instantânea da barra na direção vertical.
- Determine a velocidade terminal da barra e a corrente que passa no circuito quando ela se encontra neste velocidade.
- Calcule a potência dissipada pelo sistema na situa do item (c) e mostre que ela é igual à potência fornecida ao sistema pelo campo gravitacional.
A Lei de Lenz diz que:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Mas basicamente o que nós precisamos interpretar disso é que:
Se o fluxo do campo magnético está aumentando, o campo induzido tenta atrapalhar ele (corrente no sentido horário). Se o fluxo está diminuindo, o campo induzido tenta ajudar ele (corrente no sentido anti-horário).
Ok! O fluxo do campo magnético é dado por (no caso de um campo magnético uniforme):
O campo magnético é constante e está entrando na folha, portanto, ele é negativo.
Como a barra está descendo, a área está aumentando, isso faz com que a variação da área com o tempo seja positiva:
Logo:
Opa! Como o fluxo do campo magnético está diminuindo, a corrente estará no sentido anti-horário.
Passo 2
Pela Lei de Faraday:
Opa! Já fizemos quase todo o trabalho no passo anterior. Vimos antes que:
A área será dada por . Onde é a largura a barra (e do circuito), e é a altura do circuito.
Passo 3
A força magnética sobre a barra é dada por:
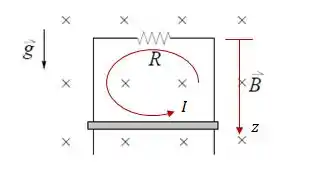
Lembrando que terá o sentido da corrente que passa pela barra. Logo, pela regra da mão direita:
Pela segunda lei de Newton:
Ah! Nós podemos associar a corrente com a fem calculada por:
Onde , logo:
Voltando para a segunda Lei de Newton:
A barra alcançará a velocidade terminal quando . Logo:
Para calcular a corrente, basta jogar na fórmula que escrevemos logo aqui em cima:
Passo 4
Por definição:
Na letra (c), nós calculamos a corrente terminal. Logo:
Para a potência gravitacional:
Resposta
- Sentido anti-horário.