Um campo eletrostático é definido por:
Onde , e são constantes positivas. Considere abaixo:
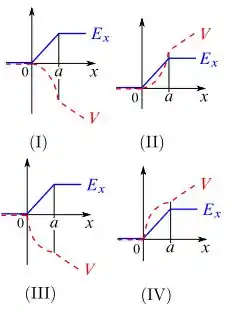
Supondo que o potencial se anula na origem, qual deles melhor representa ?
- O gráfico (I)
- O gráfico (II)
- O gráfico (III)
- O gráfico (IV)
- Nenhum deles
Passo 1
Bem... Para essa questão, temos que usar o fato de que o campo elétrico sempre pode ser escrito em termos do gradiente do potencial, isto é...
O vetor gradiente pela matemática é o vetor de derivadas...
Como o campo elétrico é , ou seja, só tem a componente ...
Ou seja...
Usando isso aí, vamos para a questão!
Passo 2
Sabemos que o campo elétrico é divido em três trechos (intervalos)...
Então para o intervalo ...
Onde é uma constante, ou seja, o potencial é uma constante qualquer que pode ser inclusive...
Passo 3
Para o intervalo de ...
Só que o potencial não pode ser descontínuo, então para o potencial em ainda ser (ou seja, ser contínuo)...
Passo 4
Depois de o campo elétrico passa a ser constante...
Ou seja, nesse momento o potencial passa a ser uma reta decrescente!
Passo 5
Agora vamos analisar as opções baseado no resultado que obtivemos...
E as opções são...
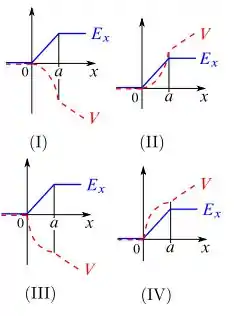
Repare que a única que possui uma parábola decrescente (com a concavidade para baixo) e negativa é a primeira opção!...
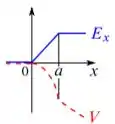
Resposta
Letra A.