Considere uma espira retangular de lado maior e de lado menor , situada no plano xy (veja figura abaixo). Aplica-se um campo magnético externo que varia no tempo de acordo com a expressão , onde é uma constante dada em e é o tempo em .
(a) Calcule a magnitude do fluxo magnético, através da espira.
(b) (1,0 ponto) Qual é o sentido da corrente induzida na espira (horário ou anti-horário)? Justifique sua resposta!
(c) (0,5 ponto) Supondo que a espira tenha resistência , calcule a magnitude da corrente induzida, , em um instante qualquer.
Passo 1
Cara, nesse problema daqui vamos ter que...
- Na letra A, calcular o fluxo do campo magnético dentro da espira. O que pode ser feito usando a definição de fluxo...
- Na letra B, já vamos ter que definir o sentido da corrente na espira o que pode ser feito usando a lei de Lenz.
- Na letra C, por sua vez teremos que primeiro encontrar a induzida na espira (usando a Lei de Faraday) e depois calcularmos a corrente por lei de Ohm...
Vamos nessa?
Passo 2
Cara, repare que a nossa espira possui uma região plana onde o vetor de direção da área (vetor perpendicular a área), no caso tem o sentido da direção ...
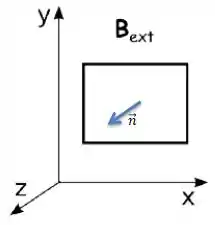
Então, podemos dizer que...
Ou ainda...
Logo, o produto escalar entre o campo magnético e o vetor normal ...
Logo, a integral de superfície se resume a uma...
ORA! A integral de , de acordo com a nossa teoria de calculo, representa a área da superfície (do retângulo de lado e )...
Logo, a magnitude do fluxo é...
Passo 3
Ora... Aqui temos que discutir um pouquinho sobre a Lei de Lenz...
A lei de Lenz nos fala que em uma espira imersa em um campo magnético externo cujo fluxo varia com o tempo , surge na espira uma corrente de modo que o campo magnético induzido por essa corrente se opõe a variação do fluxo externo.
Então, se na nossa espira temos um fluxo de um campo externo que aumenta na direção positiva do eixo , a corrente induzida tem que ser de modo que reduza esse fluxo, ou seja, ela deve circular no sentido horário. Assim, pela regra da mão direita...
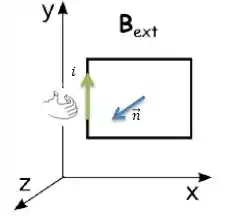
O fluxo induzido terá sentido para dentro (em ) e portanto ele vai se opor ao variação externa, como nos diz Lenz, saca?
Passo 4
Com o fluxo do campo magnético calculado, podemos então determinar a força eletromotriz pela derivada da Lei de Faraday...
Logo, a corrente induzida em função do tempo será...
Como ele nos pede o módulo da corrente em um instante qualquer, vamos pegar no instante ...
Resposta
Letra A:
Letra B: Sentido Horário pela Lei de Lenz.
Letra C: