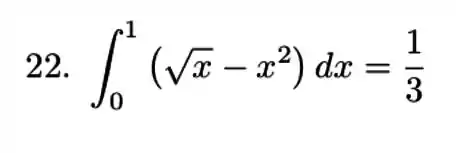Passo 1
Não precisamos necessariamente fazer o gráfico para calcular a área entre as curvas, mas é legal para dar uma ideia do nosso problema, olha aqui como ficaria nesse caso
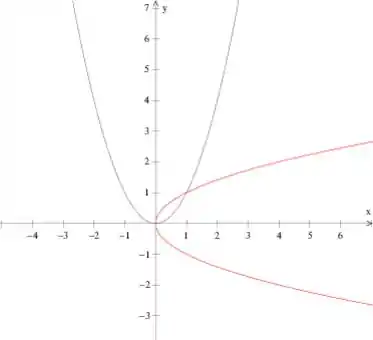
Precisamos calcular o conjunto de pontos entre essas curvas, que é o mesmo que dizer que precisamos calcular a área comum às duas curvas. Vamos lá!
Passo 2
Para começar precisamos encontrar os pontos de intersecção (encontro) entre as curvas.
Esses são os pontos de intersecção entre as curvas e serão nossos limites de integração.
Passo 3
Agora temos que montar nosso problema e resolver a integral para encontrar a área entre as curvas.
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x