ME03) A área da região delimitada pelos gráficos de e é
Passo 1
Bora lá, a primeira coisa a fazer é checar pontos interessantes das curvas. No caso, esses pontos vão ser os pontos onde elas encontram os eixos e elas mesmas. Pra , temos:
A função vai encontrar então o eixo nos pontos:
E vai encontrar o eixo quando:
Pra , como é só uma reta, temos que a origem é o único ponto de interseção com os eixos. Beleza, agora que vimos isso, vamos ver quando essas curvas vão se encontrar. Igualando elas:
Como é uma reta e um polinômio de segundo grau, que parece um copo com boca pra cima, já que temos multiplicando o termo de maior grau, esboçamos o gráfico:
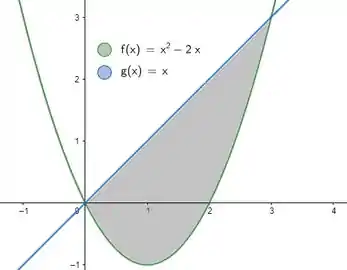
Olhando pro nosso esboço, podemos escrever a área da região delimitada (marcada em cinza) em duas parcelas: uma de até e outra de até . Vamos fazer isso porque na primeira parcela parte da área está abaixo do eixo . Vamos ter:
O que é o mesmo que:
Passo 2
Agora é mão na massa galera. A integral vai ficar: