Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 311234567891011121314151617181920212223242526272829303233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Área entre Curvas

Calcule a área da região indicada na figura abaixo, onde r corresponde a reta y = - x + 1 e f x = x 3 + x 2 - 2 x :

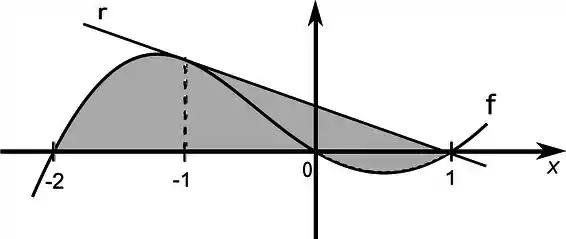
Passo 1

Como podemos ver no desenho, entre - 2 e - 1 a área vai de f x até o eixo x . Entre x = - 1 e x = 0 vai da reta r até o mesmo eixo. Já entre x = 0 e x = 1 a área fica entre a reta e f . Armando a equação da integral da área, temos:

A = ∫ - 2 - 1 f x d x + ∫ - 1 0 r x d x + ∫ 0 1 r x - f x d x

= ∫ - 2 - 1 x 3 + x 2 - 2 x d x + ∫ - 1 0 - x + 1 d x + ∫ 0 1 - x + 1 - x 3 - x 2 + 2 x d x

Passo 2

Vamos resolver uma integral de cada vez:

∫ - 2 - 1 x 3 + x 2 - 2 x d x = x 4 4 + x 3 3 - x 2 [ - 1 - 2

= 1 4 + - 1 3 - 1 - 16 4 + - 8 3 - 4

= 19 12

∫ - 1 0 - x + 1 d x = - x 2 2 + x [ 0 - 1

= - 0 2 + 0 - - 1 2 - 1

= 3 2

∫ 0 1 - x + 1 - x 3 - x 2 + 2 x d x = ∫ 0 1 - x 3 - x 2 + x + 1 d x

= - x 4 4 - x 3 3 + x 2 2 + x [ 1 0

= - 1 4 - 1 3 + 1 2 + 1 - - 0 4 - 0 3 + 0 2 + 0

= 11 12

Passo 3

Agora juntamos os resultados e encerrada a questão:

A = ∫ - 2 - 1 f x d x + ∫ - 1 0 r x d x + ∫ 0 1 r x - f x d x

= 19 12 + 3 2 + 11 12

= 48 12

= 4   u . a .

Essa á a área que o cara pediu!

Resposta

A = 4   u . a .

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x